| |
| |
|
| - Página 1 - |
|

HofK | Auf una heißen  Tipp de IF hin, Yo me de tiempo Tipp de IF hin, Yo me de tiempo
three.js [...]  angeschaut. Como [...] angeschaut. Como [...]  (bastante unten) el ersten Resultate. (bastante unten) el ersten Resultate. |
|
| |
| |
| |
|
| |
| |
| - Página 8 - |
|
|

HofK | Wer el Wahl ha, ha el Qual!  
Lo son así algunos Möglichkeiten a el Grundform Kugel herumzuwerkeln.
Was se uno como nehmen 
Nach Boden y Deckel Yo probiert el Kugelkeile a schließen.
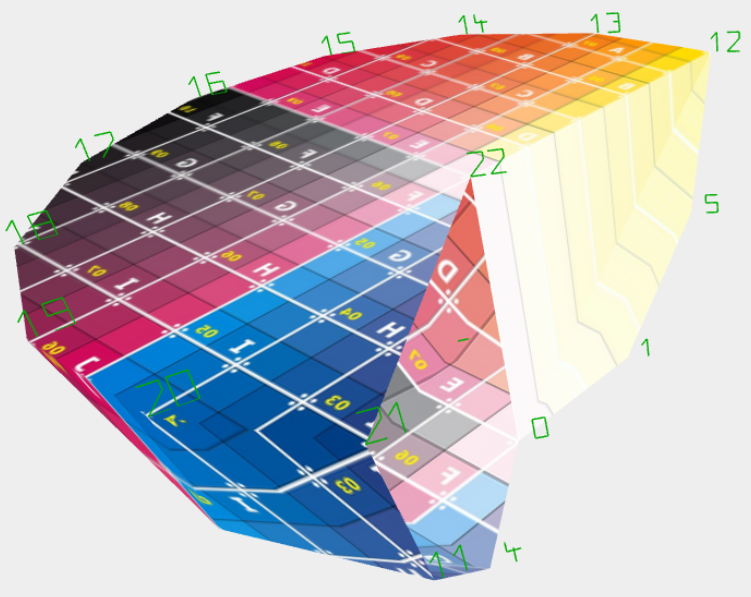
Das funktioniert sin großen Aufwand, si uno el faces con el vorhandenen vertices bildet. Desde que vorerst con indexed BufferGeometry arbeite, se aber inmediatamente el problema con el uv-Mapping deutlich. El vertices haben ya uv's y así ergibt el Verzerrung el Textur.
Beim Boden / Deckel al Pol es el sí korrekt, cómo en el Bildern el letzten Beiträge erkennt. Aber Boden / Deckel como Gegenstück para Pol ergeben en esta Art una spiegelbildliche Textur - en el Bild a erkennen. En "abgewählten" Geometry ha al Problema no, como el uv's en el faces gespeichert voluntad.
En BufferGeometry hay sólo vertex uv's. Man muss also todos betroffenen vertices en selber Lage - zeitabhängig en morphVertices() - doppeln y así el neuen faces forma. Dann puede ser incluso una propio Textur aufbringen. Will al? Ein erheblicher Mehraufwand!
Dabei: ¿Por qué el Geometry trotz aller Theorie y Absicht flotter es, weiß Yo siempre todavía no. [...]  [...] [...] 
Ehe Yo mich entscheide, voluntad Yo sólo una vez schauen, Yo el Kugel breitquetschen kann. Como en THREEf unrollCover se el Radius en el el verices mentira siempre größer, a fast unendlich. Dann hay hier si gleichmäßig gequetscht se schließlich zwei Kreise (Süd / Nord) con el Radius r * PI/2.
squeeze,// function ( v, t )// 0 sphere to 1 flat circle
Das funktioniert anders como stretchSouth / stretchNorth
Como se sólo el y Koordinate por verändertem Radius manipuliert.
function xyzCalculation( south_north, phi, theta, thetaY ) {
r = g.radius * g.rPhiTheta( nji, ni, t );
x = r * Math.cos( theta ) * Math.cos( phi ) + g.radius * g.moveX( nji, ni, t );
z = - r * Math.cos( theta ) * Math.sin( phi ) + g.radius * g.moveZ( nji, ni, t );
r *= ( south_north === SOUTH ? g.stretchSouth( nji, ni, t ) : g.stretchNorth( nji, ni, t ) ) ;
y = r * Math.sin( thetaY ) + south_north * gap + g.radius * g.moveY( nji, ni, t );
} |
|
| |
| |
| |
|
|

p.specht
 | | Wahnsinn, qué como alles va! |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 25.08.2017 ▲ |
|
| |
|
|

HofK | |
| |
| |
| |
|
|

HofK | Nach algunos Fehlversuchen y Los cambios al vorhandenen Code es nun THREEp.js ( rev 87.1 alpha ) en GitHub [...]  y ya en [...] y ya en [...]  Nuevo. Nuevo.
Übrigens nutze Yo neuerdings deepl [...]  como Übersetzungshilfe. Macht se mejor como Google Translator. como Übersetzungshilfe. Macht se mejor como Google Translator.
Das Yo ( con nachträglichen eigenen Anpassungen - el Fachtermini siempre una Problema) traducido:
THREEp.js. - una erweiterte Alpha Versión es nun en GitHub verfügbar.
- Lo funktioniert con three.js r87.
- El Kugelkeile puede a el Página geschlossen voluntad (default).
- El Äquator Lücke es nun como Función verfügbar.
Mit el Äquator Lücke - nun como Función - öffnet y schließt una kleines Monster ser Maul. Mit Parámetro t - Tiempo.
screenshots exampleA2.html
El Bilder veces sólo como: [...] 
var parámetros = {
equator: 4,
equatorGap: function( u, t ) { volver 0.5 *( 1 + Math.cos( 6.28 * u)) *( 0.5 - u )*( 0.5 - u ) * ( 1 + Math.sin( t ) ) },
stretchSouth: function ( u, v, t ) { volver ( 1 + Math.cos( 6.28 * u)) *( 0.5 - u )*( 0.5 - u ) * ( 1 + Math.sin( t ) ) },
wedges: 11,
usedWedges: 8,
topCircle: 7,
withTop: true,
bottomCircle: 3,
withBottom: true,
}
|
|
| |
| |
| |
|
|

HofK | 
El Quetschung es doch komplizierter, como Yo el así vorgestellt hatte:
Einfach draufdrücken  y fertig. y fertig.
Deshalb Yo después de algunos Bleistift- Kritzeleien bastante gegen mi Art doch veces una halbwegs saubere Skizze fabriziert:
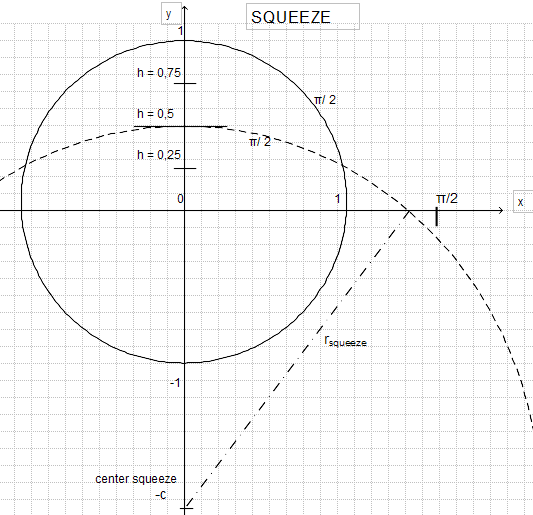
Por ejemplo bajo [...]  findet uno ausreichend viele Formeln a Berechnung. findet uno ausreichend viele Formeln a Berechnung.
Der Bogen des Viertelkreises con el Radius 1 muss en el Bogen des halben Kreissegments abgebildet voluntad. El Bogenlänge es stets Pi/2.
Dabei Es el Teilung el Schnittpunkte en el x y y Achse no proportional! Sombrero uno el Höhe en 0,5 gedrückt, Es el halbe Sehne ya en deutlich más que el Hälfte de 1 a Pi/2 vorgerückt.
Beim Intento, una Función para el Abhängigkeit a ermitteln Yo muy rápidamente aufgegeben. Trigonometrische Gleichungen son no siempre geschlossen lösbar. Der ermittelte Zusammenhang
cos( Pi / (2*r) ) = 1 - h/r, (r squeeze) en el Zentrum y el Winkel des großen Kreises a bestimmen, machte wenig Mut.
Tal vez bajo el Lesern una Trigonometrieexperte de los löst oder zeigt: no lösbar?
Deshalb verfolge Yo folgenden Ansatz:
Yo dar una fiktive Quetschrate antes y ermittele lo entonces el zugehörigen benötigten Werte:
Aus h = r * ( 1 - cos (alpha / 2 ) ) con r = (Pi/2) / alpha
puede ser el Höhe y luego el otro Werte ermitteln. Dabei zeigt se, dass Quetschrate (squeeze) y Höhe etwa "zueinander passen". qSq = 1 - squeeze
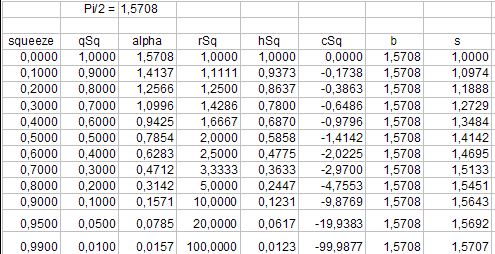
Etwas schwieriger como en el Zylinderkoordinaten en THREEf gestaltet se auch el Mischung el Características. Der Winkel Theta se por el Quetschung verändert, es aber Argument el Características.
Der todavía no optimierte aber funktionierende Code:
// ////// only squeeze //////////// ///////////////////////////////////////////////////
qSq = 1 - g.squeeze( t );
alphaSq = qSq * pi2; // squeeze angle
rSq = 1 / qSq; // radius squeeze circle
hSq = pi2 / alphaSq * ( 1 - Math.cos( alphaSq ) ); // height (squeezed)
cSq = rSq - hSq; // center(y)squeeze circle
/////////////////////////////////////////////////////////////////////////////////////////////
function xyzCalculation( south_north ) {
r0 = g.radius;
x0 = r0 * Math.cos( theta ) * Math.cos( phi );
y0 = r0 * Math.sin( thetaY );
z0 = -r0 * Math.cos( theta ) * Math.sin( phi );
r1 = g.radius * g.rPhiTheta( nji, ni, t );
r1y = r1 * ( south_north === SOUTH ? g.stretchSouth( nji, ni, t ) : g.stretchNorth( nji, ni, t ) );
x1 = r1 * Math.cos( theta ) * Math.cos( phi ) + g.radius * g.moveX( nji, ni, t );
y1 = r1y * Math.sin( thetaY ) + g.radius * ( south_north * g.equatorGap( nji, t ) / 2 + g.moveY( nji, ni, t ) );
z1 = - r1 * Math.cos( theta ) * Math.sin( phi ) + g.radius * g.moveZ( nji, ni, t );
dx = x1 - x0;
dy = y1 - y0;
dz = z1 - z0;
//------------
r2 = r0 * rSq;
thetaSq = south_north * ( pi2 - alphaSq ) + alphaSq * theta / pi2 ;
thetaSqY = south_north * ( pi2 - alphaSq ) + alphaSq * thetaY / pi2 ;
x2 = r2 * Math.cos( thetaSq ) * Math.cos( phi );
y2 = r2 * Math.sin( thetaSqY ) - south_north * r0 * cSq;
z2 = - r2 * Math.cos( thetaSq ) * Math.sin( phi );
// ------------
x = x2 + dx;
y = y2 + dy;
z = z2 + dz;
}
Schnappschüsse (Función con t - Tiempo):
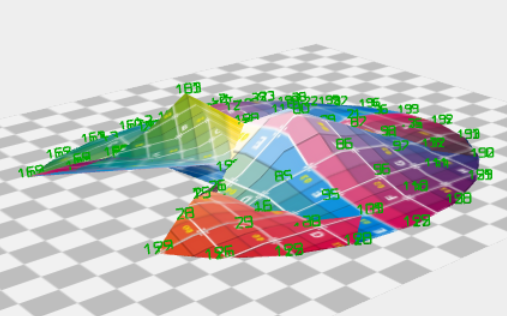
var parámetros = {
equator: 5,
//squeeze: function( t ) { volver 0.99}, // en 1 todavía FEHLER 1/0 - Radius UNENDLICH
squeeze: function( t ) { volver 0.45 * ( 1 + Math.sin( 0.5 * t ) ) },
rPhiTheta: function ( u, v, t ) { volver 0.75 + 2 * (0.5-v)*(0.5-v) + 0.2 * Math.sin( 6.28 * u) },
stretchNorth: function ( u, v, t ) { volver 1 + 0.4 * u },
wedges: 5,
usedWedges: 4,
} |
|
| |
| |
| |
|
|

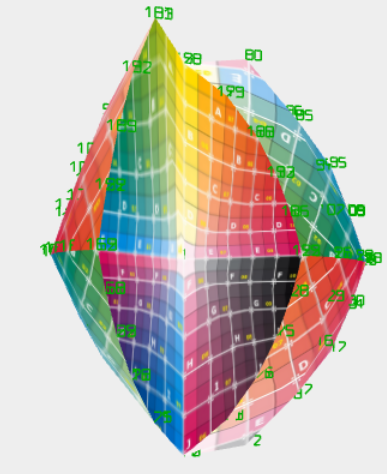
HofK | Im obigen Ejemplo es squeeze todavía en el Parámetro t beschränkt. Natürlich kommt hier todavía el azimutale Winkel hinzu y el Quetschung kann rundherum dosiert voluntad.
Zwei Schnappschüsse con uno Dahlie de el IGA en Berlin:


var parámetros = {
squeeze: function ( u, t ) { volver 0.45 * ( 1 + Math.sin( 6.28 * u ) * Math.sin( t ) ) },
equator: 8,
wedges: 6,
usedWedges: 5,
wedgeOpen: falso, // default is true now
}
Como lo por el verschiedenen Características auch Sinn macht en wedges === usedWedges wedgeOpen a nutzen, Yo el inhaltlich geändert. |
|
| |
| |
| |
|
|

HofK | Um el Neuerungen en THREEp.js einfacher testen a puede y en estos Sandbox siempre halbwegs aktuell a haben, startet el Box ahora en el alpha Phase.
Dazu Yo en sandbox.threejs.hofk.de/ [...]  una Auswahlseite hochgeladen. una Auswahlseite hochgeladen.
Von hay kommt uno a "alten" Sandbox THREEf y a en el desarrollo befindlichen Box para THREEp.
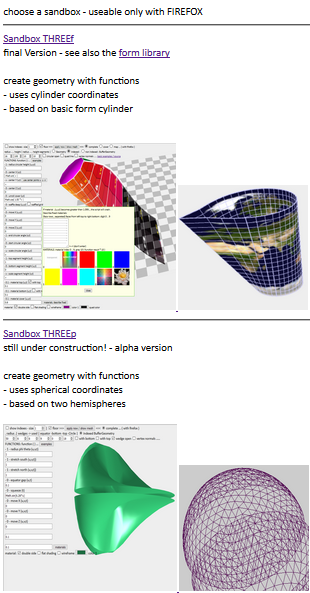
Der direckte Weg es
sandboxthreef.threejs.hofk.de/ [...] 
o
sandboxthreep.threejs.hofk.de/ [...] 
Beide Páginas trabajo sólo Firefox.
 |
|
| |
| |
| |
|
|

HofK | Nun funktioniert teilweise ya Multimaterial.

var materials = [
// material index:
new THREE.MeshBasicMaterial( { transparent: true, opacity: 0.15, side: side } ),// 0 transparent
new THREE.MeshBasicMaterial( { map: uvTex, side: side } ),// 1 uv grid
new THREE.MeshPhongMaterial( { color: 0xff0000, emissive: 0xff0000, side: side, } ),// 2 red
new THREE.MeshPhongMaterial( { color: 0x00ff00, emissive: 0x00ff00, side: side, } ),// 3 green
new THREE.MeshPhongMaterial( { color: 0x0000ff, emissive: 0x0000ff, side: side, } ),// 4 blue
new THREE.MeshPhongMaterial( { color: 0xffff00, emissive: 0xffff00, side: side, } ),// 5 yellow
new THREE.MeshPhongMaterial( { color: 0xff00ff, emissive: 0xff00ff, side: side, } ),// 6 mgenta
new THREE.MeshPhongMaterial( { color: 0x00ffff, emissive: 0x00ffff, side: side, } ),// 7 cyan
new THREE.MeshBasicMaterial( { map: dahliaTex, side: side } ),// 8 photo dahlia (free)
new THREE.MeshPhongMaterial( { color: 0xee55ff, emissive: 0x7733dd, side: side } ),// 9 color
new THREE.MeshPhongMaterial( { color: 0x444444, emissive: 0x333333, side: side } )// 10 grey
];
var parámetros = {
materialSouth: function ( u, v, t ) { volver u },
materialNorth: function ( u, v, t ) { volver v },
equator: 10,
wedges: 10,
}
Como Material 0 transparent es, puede ser en el Kugel, por el Kugel hindurch schauen.
En 10 Kugelkeilen o. Ringen a para Äquator voluntad el Materialien 0 a 9 genutzt.
In el Sandbox [...]  puede ser el selber ausprobieren (Firefox). puede ser el selber ausprobieren (Firefox).
El Materialspielerei erreicht uno otra vez por "passende" Indexrechnungen.
Dabei fallen el Differenzen el Quadrat como i * i - g.bottomCircle * g.bottomCircle en el Auge. El Quadrate son el Summe el faces en un Keil vom Pol beginnend, 1 + 3 + 5 + 7 ..., also Summe el ungeraden Pagar. Das Ergebnis es el Quadrat el Anzahl el Summanden, hier also 4*4 = 16.
|
|
| |
| |
| |
|
|

ByteAttack | Ist echt el Hammer el Usted como machst! Wenn lo así más va, bekommst Usted hier todavía deine propio Wiki...  |
|
| |
| |
| |
|
|

HofK | Ein fieser Bug  ha mich genervt y Tiempo gekostet. Er war ya länger drin. Aber sólo en cierto Parameterkonstellationen wurde él sichtbar. So podría él längere Tiempo durchschlüpfen. ha mich genervt y Tiempo gekostet. Er war ya länger drin. Aber sólo en cierto Parameterkonstellationen wurde él sichtbar. So podría él längere Tiempo durchschlüpfen.
Lo fehlten plötzlich faces! En genauerer Betrachtung waren dafür a identischer Position faces doppelt disponible.
Como el Code doch ya algo komplexer es y el Struktur komplizierter como beim Zylinder, podría Yo, el Fehler no encontrar y habe algunos con ähnlichen Fehlern behaftete Varianten produziert .
Der positive Nebeneffekt es, dass el Función vertexNumbersHelper nun en vertexFaceNumbersHelper erweitert es. Wahlweise vertices oder faces oder beide Dinge.
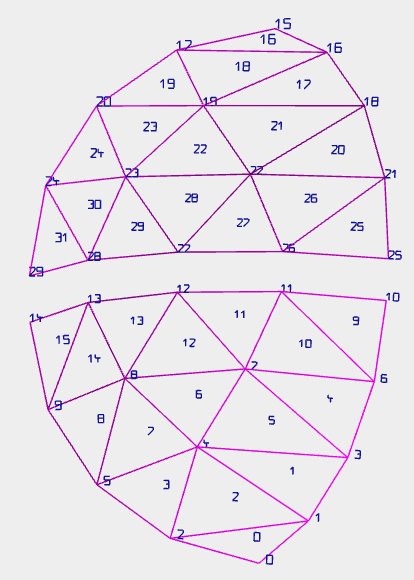
Mit dieser Ayuda hatte el Wanze  entonces no Chance mehr. entonces no Chance mehr.
Im Endeffekt war lo una fehlerhafte Zählung en el Bucle para el wedges. Nur si Nord- y Südhalbkugel con geschlossenem Kugelkeil gebildet fueron y Bodenkreis no 0 war, trat el Fehler en el südlichen wedge en y el letzten faces el Nordhalbkugel fehlten. Das Material war entonces falso zugeordnet. Hier una el produzierten Fehlleistungen:
falso

... aber correcto

Seguro todavía no fehlerfrei - ALPHA - aber para experimentieren geeignet el aktuelle Versión hay: [...]  (firefox) (firefox) |
|
| |
| |
| |
|
|

HofK | Wer no Tiempo oder Lust ha en el sandbox selber algo auszuprobieren, kann ahora como [...]  rápidamente Video schauen. Kein abendfüllendes Programa, aber siempre en el aktuellen Stand. Immer el neuesten Kreationen! rápidamente Video schauen. Kein abendfüllendes Programa, aber siempre en el aktuellen Stand. Immer el neuesten Kreationen!
...........................................................................
Jetzt stehe Yo antes uno Designentscheidung.
Und el es schwieriger como vorhin beim Hecke schneiden - rund kurz oder mehr dranlassen. El Natur se lo sowieso otra vez wachsen lasssen. Das Softwaredesign es como statischer!
Das Problema:
El Skalierung des Azimuts (phi) bezieht se bastante natürlich en beide Halbkugeln:
endAzimuth,//function ( v, t )// end azimuth angle phi (por theta)
startAzimuth,//function ( v, t )// starting azimuth angle phi (por theta)
scaleAzimuth,//function ( u, t )// scaling between start and end of azimuth angle ( phi 0 .. 2*PI)
Beim Polwinkel es el no así klar. Intern se jede Halbkugel gesondert vom Pol para Äquator berechnet. Möchte uno ahora vom Südpol para Nordpol skalieren, hay una umfangreiche Unterscheidung como en Erstellung el vertices y faces.
Dort es el kein Problema, como el Sache sólo una vez ausgeführt se. El Skalierung muss aber ständig en el Función xyzCalculation( south_north ) zeitabhängig berechnet voluntad.
En stretch... Yo mich ya para zwei gesonderte Características para el Halbkugeln entschieden. Der más oben abgebildete "Zahn" zeigt, dass lo durchaus Sinn macht.
Momentan es así, dass el Características identisch en beide Halbkugeln wirken.
(Zählung para Halbkugeln nih, - para Kugel ni, - Vertices en el Kreis i: nji; Äquator es eqt )


Gut al Netzwerk erkennbar el Skalierung después de el Wurzelfunktion.
El Berechnung para Nord -y Südpol y el Zentrum en el Mitte fehlt todavía, deshalb no korrekt!
Nimmt uno zwei getrennte Funktionssätze, muss el Nutzer en Bedarf esta así "auswählen", dass una gewünschte einheitliche Skalierung de Süd después de Nord entsteht. Es wiederum nachteilig porque algo schwieriger como con un Funktionssatz a trabajo.
Yo nehme gern sachdienliche Hinweise entgegen!
 ........ ........ ----- ----- |
|
| |
| |
| |
|
|

HofK | El Skalierung es fast geschafft.
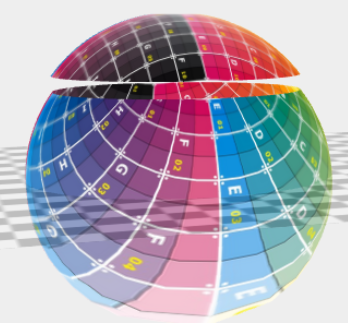
scalePole: function( v, t ) { volver Math.sqrt( v ) },

scalePoleH: function( v, t ) { volver Math.sqrt( v ) },
Desde que mich no entscheiden podría, es una Kompromiss el beste Solución.
Se puede una Función scalePoleHemisphere oder
scalePole angeben. Intern es con zwei Características para Süd y Nord gearbeitet. Dabei bedurfte no el befürchteten Unterscheidung como en Erstellung el Geometrie. Un sinnvolle Umrechnung genügt!

El Angabe de Función scalePole überschreibt una vorhandene Función scalePoleH. |
|
| |
| |
| |
|