PHP, HTML & JavaScript- Forum | | | | | | - Seite 1 - |
| 
HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
| | | | | | |
| | | | | | - Seite 7 - |
| | 
HofK | Um zu schauen, ob die Farbgestaltung Einfluss auf die Geschwindigkeit nimmt, habe ich noch die Auswahlmöglichkeiten multicolor und monochrome hinzugefügt. Bei monochrome werden dann nur noch die vertices, manipuliert (Form), die Farbgebung per
if ( multicolor ) { ... } ausgeblendet.

Das ändert aber nichts am Ergebnis. [...]  |
| | | | | | |
| | 
HofK | Nachdem THREEf.js ersteinmal soweit komplett ist, habe ich mal geschaut, wie es in Richtung Polarkoordinaten weitergehen könnte.
Dazu benötigt man eine Kugel. In three.js ist eine Kugel (sphere) nach dem üblichen System mit Längen- und Breitengraden definiert. Beispiel [...] 
Weiterhin ergeben Tetraeder (Tetrahedron), Oktaeder (Octahedron), Dodekaeder (Dodecahedron), Ikosaeder (Icosahedron), mit dem Parameter Detail größer 0 Kugeln mit entsprechender Genauigkeit. Diese werden durch Projektion der Ecken der Figur auf eine Kugel und anschließende Aufteilung (Detail) erzeugt. Dazu wird die auch gesondert verwendbare "Geometrie" Polyhedron [...]  intern benutzt. intern benutzt.
Ich wollte erst einmal eine Halbkugel (Hemisphere) erzeugen.
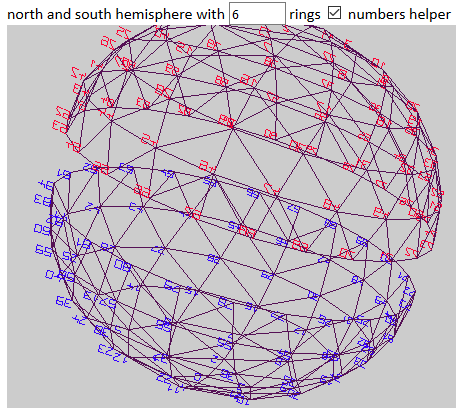
Ausgehend vom Pol habe ich entsprechend dem Oktaeder 4 Ecken erzeugt, d.h keine Teilung der (ebenen) Quadranten vorgenommen. Der nächste Ring entsteht, indem mittig (45°) geteilt wird, es entstehen 8 Ecken. Dann wird zweimal geteilt ( 30°, 60°) und es entstehen 12 Ecken.
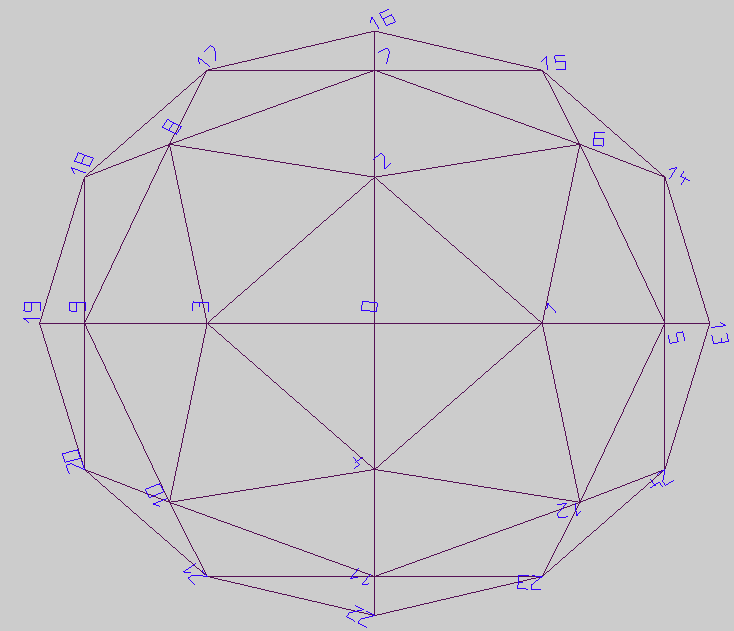
Durch verbinden der Ecken gibt es 4, 12, 20 Dreiecke. Dahinter stecken recht einfache Formeln. Also habe ich die Ecken (vertices) ringweise fortlaufend erzeugt und dann so auch die Flächen (faces).
Doppelt verschachtelte Schleifen hatte ich schon genug, hier benötigt man mal eine dreifache Verschachtelung.
Da die ganze Sache quadrantenweise funktioniert (je Quadrant 1, 2, 3, 4, 5 ... Ecken und (1), 3, 5, 7, 9, 11 ... Flächen) ist die Zuordnung der Eckpunkte der Flächen vom Quadranten mit abhängig. Dafür ist die eigentliche Berechnung der Eckpunkte a, b, c dann "sehr einfach" möglich.
rvSum = 1; // only vertex 0
for ( var i = 1; i < rs; i ++ ) {
for ( var q = 0; q < 4; q ++ ) { // quarter ring
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face in quarter
a = rvSum;
b = a + 4 * i + q;
c = b + 1;
g.faces.push( new THREE.Face3( a, b, c ) );
} else {
// two faces / vertex
a = j + rvSum;
b = a - 1;
c = a + 4 * i + q;
if ( q === 3 && j === i ) a = a - 4 * i; // connect to first vertex of circle
g.faces.push( new THREE.Face3( a, b, c ) );
// a from first face
b = c; // from first face
c = b + 1;
if ( q === 3 && j === i ) c = c - 4 * ( i + 1 ); // connect to first vertex of next circle
g.faces.push( new THREE.Face3( a, b, c ) );
}
}
rvSum += i;
}
}
Ausprobieren kann man die Halbkugeln mit Wahl der Ringe und bei Bedarf mit Nummerierung der Ecken unter [...]  bzw. [...] bzw. [...] 
Sogar 0 Ringe geht, eine Gerade zum Pol!
Weil es so schön einfach ist, habe ich erst einmal Geometry benutzt. Buffer wird natürlich nachgereicht. |
| | | | | | |
| | 
HofK | Wenn die Halbkugel mit einer Vierteilung funktioniert, muss es doch auch mit drei Teilen klappen. Passt auch besser zu den Dreiecken im Raum.
Tatsächlich lässt sich das Verfahren ganz analog übernehmen.
Es gibt dann keine Pol Ecke, sondern ein Pol Dreieck. Damit wird es im Algorithmus sogar noch einfacher, die Sonderbehandlung verringert sich von vier auf ein Dreieck am Anfang. Bei den Schleifen nimmt man dann den Faktor 3 statt 4, z.B. 3 * i.
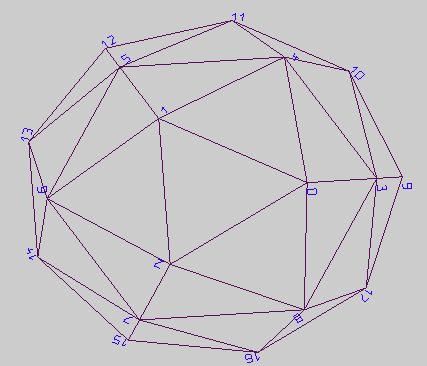
Einfach anschauen und ausprobieren unter [...]  bzw. [...] bzw. [...] 
Jetzt ist die sechsfache Teilung - wieder mit Polecke - an der Reihe. |
| | | | | | |
| | 
HofK | Wenn 3, 4 und 6 Teile gehen, dann gehen auch (fast) beliebig viele Teilungen des Äquators - mal austesten bis der Browser qualmt  . .
Deshalb gibt es neben der sehr schönen Sechsteilung auch gleich die allgemeine Variante.
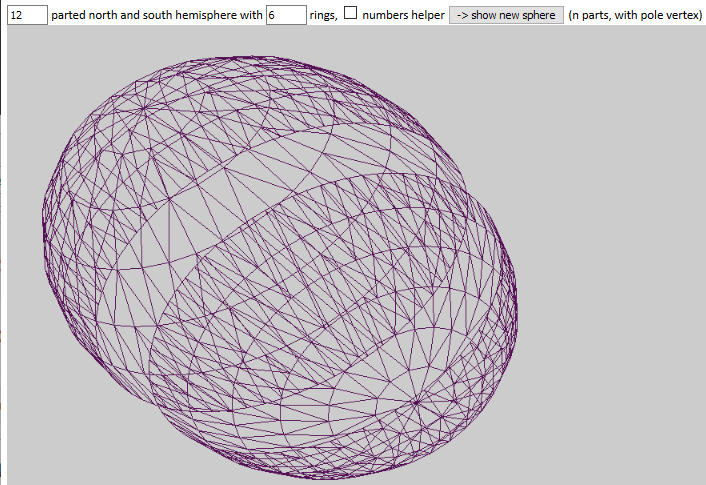
Siehe [...] 
- [...]  ( update: 26.07.) ( update: 26.07.)
bzw: [...]  |
| | | | | | |
| | 
HofK | HofK (23.07.2017)
Weil es so schön einfach ist, habe ich erst einmal Geometry benutzt. Buffer wird natürlich nachgereicht.
Versprechen soll man einhalten.
Deshalb nun das Update zum gestrigen Programm mit  BufferGeometry. [...] BufferGeometry. [...]  |
| | | | | | |
| | 
HofK | Mit einigen kleinen Änderungen und Ergänzungen lassen sich nun auch Kugelschichten, Kugelzonen erzeugen. Erst einmal nur innerhalb einer Halbkugel.
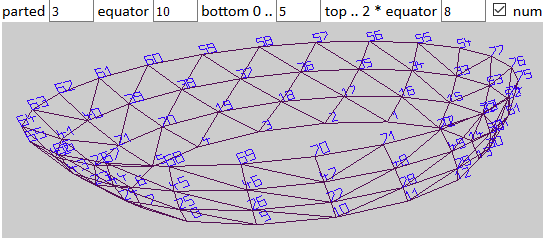
Geht es nämlich über den Äquator, steht mir noch eine Art "Äquatortaufe" bevor. Dann muss ab dem Äquator rückwärts gerechnet werden, die Anzahl der vertices und faces wird wieder kleiner.
Die aktuelle Arbeitsversion gibt es in zwei Quelltextboxen.
Einfach das Script dann statt // ... siehe unten ... in die HTML Datei einkopieren.
Dann noch die zusätzlich benötigten Scripte
<script src="../js/three.min.86.js"></script>
<script src="../js/OrbitControls.js"></script>
<script src="../js/THREEx.WindowResize.js"></script>
in den richtigen Ordner packen.
Oder in den selben Ordner und ../js/ löschen.
'use strict'
// !!!!! Debug !!!!!
var debug = document.getElementById("debug"); // !!!!! Debug !!!!!
var scene = new THREE.Scene();
var camera = new THREE.PerspectiveCamera(45,160/ 90 , 0.1, 100000);
camera.position.set(0,0,250);
var renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth,window.innerHeight);
renderer.setClearColor(0xcccccc);
document.body.appendChild(renderer.domElement);
THREEx.WindowResize(renderer, camera);
var controls = new THREE.OrbitControls( camera, renderer.domElement );
var clock = new THREE.Clock( true );
var time;
var g;
var sphere;
var radius;
var bottomCircle, equator, topCircle;
//var rings;
var parts // radial parts
var rvSum; // sum of ring vertices
var vertexCount;
var faceCount;
//var vertexOffset;
//var faceOffset;
var x, y, z;
var a, b, c;
var ni, nji; // relative i, j
var Alpha;
var sinAlpha;
var cosAlpha;
var vertexNumbersHelperSphere;
var vertices; // for BufferGeometry / Helper
var faceIndices;
var showGeo = false;
var material = new THREE.MeshBasicMaterial( { color: 0x551155, side: THREE.DoubleSide, wireframe: true } );
document.getElementById( "show" ).onclick = showNewSphere;
animate();
//..............
function showNewSphere() {
if ( sphere ) {
if ( vertexNumbersHelperSphere ) sphere.remove( vertexNumbersHelperSphere );
scene.remove( sphere);
g.dispose();
showGeo = false;
}
// Geometry or BufferGeometry
if ( document.getElementById( "Geometry" ).checked ) g = new THREE.Geometry();
if ( document.getElementById( "BufferGeometry" ).checked ) g = new THREE.BufferGeometry();
radius = 50;
parts = Math.floor( document.getElementById( "parts" ).value );
bottomCircle = Math.floor( document.getElementById( "bottomCircle" ).value );
topCircle = Math.floor( document.getElementById( "topCircle" ).value );
equator = Math.floor( document.getElementById( "equator" ).value );
// rings = topCircle - bottomCircle;
//vertexOffset = 1 + parts * ( bottomCircle - 1 ) * bottomCircle / 2 ;
//faceOffset = parts * bottomCircle * bottomCircle;
// !!!!! D E B U G !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
//debug.value = ;
vertexCount = 0;
for ( var i = bottomCircle; i <= topCircle; i ++ ) {
vertexCount += i <= equator ? i : equator * 2 - i;
}
vertexCount *= parts;
vertexCount += bottomCircle === 0 ? 1 : 0; // south pole
vertexCount += topCircle === equator * 2 ? 1 : 0; // north pole
// faceCount = parts * rings * rings;
faceCount = 0;
for ( var i = bottomCircle; i < topCircle; i ++ ) {
faceCount += i < equator ? 2 * i + 1 : 2 * ( equator * 2 - i - 1 ) + 1;
}
faceCount *= parts;
if ( g.isGeometry ) {
for ( var i = 0; i < vertexCount; i ++ ) {
g.vertices.push( new THREE.Vector3( 0, 0, 0 ) );
}
}
if ( g.isBufferGeometry ) {
var idxCount = 0;
vertices = new Float32Array( vertexCount * 3 );
faceIndices = new Uint32Array( faceCount * 3 );
g.setIndex( new THREE.BufferAttribute( faceIndices, 1 ) );
g.addAttribute( 'position', new THREE.BufferAttribute( vertices, 3 ).setDynamic( true ) );
var posIdx;
}
rvSum = 0;
if ( bottomCircle === 0 ) {
a = 0; // vertex 0: pole
b = 1;
c = 2;
for ( j = 0; j < parts; j ++ ) {
setFace(); // Geometry or BufferGeometry
b ++;
if ( b < parts ) { c ++; } else { c = 1; }
}
rvSum = 1; // only vertex 0, south pole
}
// for ( var i = 1; i < rings; i ++ ) {
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i < topCircle; i ++ ) {
for ( var q = 0; q < parts; q ++ ) {
// rvSum = 1 + q * i + parts * ( i - 1) * i / 2;
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face in part
a = rvSum;
b = a + parts * i + q;
c = b + 1;
setFace(); // Geometry or BufferGeometry
} else {
// two faces / vertex
a = j + rvSum;
b = a - 1;
c = a + parts * i + q;
if ( q === ( parts - 1 ) && j === i ) a = a - parts * i; // connect to first vertex of circle
setFace(); // Geometry or BufferGeometry
// a from first face
b = c; // from first face
c = b + 1;
if ( q === ( parts - 1 ) && j === i ) c = c - parts * ( i + 1 ); // connect to first vertex of next circle
setFace(); // Geometry or BufferGeometry
}
}
rvSum += i;
}
}
if ( g.isGeometry ) g.vertices[ 0 ].set( 0, -radius, 0 ); // south pole
if ( g.isBufferGeometry ) {
vertices[ 0 ] = 0;
vertices[ 1 ] = -radius; // south pole
vertices[ 2 ] = 0;
}
rvSum = 0;
if ( bottomCircle === 0 ) {
rvSum = 1; // only vertex 0
if ( g.isGeometry ) g.vertices[ 0 ].set( 0, -radius, 0 ); // pole
if ( g.isBufferGeometry ) {
vertices[ 0 ] = 0;
vertices[ 1 ] = -radius;
vertices[ 2 ] = 0;
}
}
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i <= topCircle; i ++ ) {
ni = i / equator; // rings;
Alpha = Math.PI / 2 * ni;
sinAlpha = Math.sin( Alpha );
cosAlpha = Math.cos( Alpha );
for ( var j = 0; j < i * parts; j ++ ) {
nji = j / ( i * parts );
x = radius * sinAlpha * Math.cos( 2 * Math.PI * nji );
y = - radius * cosAlpha;
z = - radius * sinAlpha * Math.sin( 2 * Math.PI * nji );
if ( g.isGeometry ) g.vertices[ rvSum + j ].set( x, y, z );
if ( g.isBufferGeometry ) {
posIdx = ( rvSum + j ) * 3;
vertices[ posIdx ] = x;
vertices[ posIdx + 1 ] = y;
vertices[ posIdx + 2 ] = z;
}
}
rvSum += i * parts;
}
sphere = new THREE.Mesh( g, material );
if ( document.getElementById( "helper" ).checked ) {
vertexNumbersHelperSphere = new vertexNumbersHelper( sphere, 2.5, 0x3300ff);
vertexNumbersHelperSphere.update();
}
scene.add( sphere );
showGeo = true;
function setFace() {
if ( g.isGeometry ) {
g.faces.push( new THREE.Face3( a, b, c ) );
}
if ( g.isBufferGeometry ) {
faceIndices[ idxCount ] = a;
faceIndices[ idxCount + 1 ] = b;
faceIndices[ idxCount + 2 ] = c;
idxCount += 3;
}
}
}
function animate(){
requestAnimationFrame(animate); // rekursiver Aufruf
time = clock.getElapsedTime();
if ( showGeo ) {
//sphere.rotation.x = 0.2 * time;
//sphere.rotation.y = 0.05 * time;
}
renderer.render(scene, camera);
}
function vertexNumbersHelper( mesh, size, color ) {
var vertexNumbers = [];
var materialDigits = new THREE.LineBasicMaterial( { color: color } );
var geometryDigit = [];
var digit = [];
var d100, d10, d1; // digits
var coordDigit = []; // design of the digits
coordDigit[ 0 ] = [ 0,0, 0,9, 6,9, 6,0, 0,0 ];
coordDigit[ 1 ] = [ 0,6, 3,9, 3,0 ];
coordDigit[ 2 ] = [ 0,9, 6,9, 6,6, 0,0, 6,0 ];
coordDigit[ 3 ] = [ 0,9, 6,9, 6,5, 3,5, 6,5, 6,0, 0,0 ];
coordDigit[ 4 ] = [ 0,9, 0,5, 6,5, 3,5, 3,6, 3,0 ];
coordDigit[ 5 ] = [ 6,9, 0,9, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 6 ] = [ 6,9, 0,9, 0,0, 6,0, 6,5, 0,5 ];
coordDigit[ 7 ] = [ 0,9, 6,9, 6,6, 0,0 ];
coordDigit[ 8 ] = [ 0,0, 0,9, 6,9, 6,5, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 9 ] = [ 6,5, 0,5, 0,9, 6,9, 6,0, 0,0 ];
if ( mesh.geometry.isGeometry) {
var verticesCount = mesh.geometry.vertices.length;
for ( var i = 0; i<10; i ++ ) {
geometryDigit[ i ] = new THREE.Geometry();
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
geometryDigit[ i ].vertices.push( new THREE.Vector3( 0.1 * size * coordDigit[ i ][ 2 * j ], 0.1 * size * coordDigit[ i ][ 2 * j + 1 ], 0 ) );
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
if ( mesh.geometry.isBufferGeometry) {
var verticesCount = vertices.length / 3 ;
var digitPositions = [];
for ( var i = 0; i < 10; i ++ ) {
geometryDigit[ i ] = new THREE.BufferGeometry();
digitPositions[ i ] = new Float32Array( coordDigit[ i ].length / 2 * 3 );
geometryDigit[ i ].addAttribute( 'position', new THREE.BufferAttribute( digitPositions[ i ], 3 ) );
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
digitPositions[ i ][ j * 3 ] = 0.1 * size * coordDigit[ i ][ 2 * j ];
digitPositions[ i ][ j * 3 + 1 ] = 0.1 * size * coordDigit[ i ][ 2 * j + 1 ];
digitPositions[ i ][ j * 3 + 2 ] = 0;
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
// numbering the vertices, hundreds ...
var i100 = 0;
var i10 = 0;
var i1 = -1;
for ( var i = 0; i < verticesCount ; i ++ ) {
// Number on board, up to three digits are pinned there
if ( mesh.geometry.isGeometry) {
var board = new THREE.Mesh( new THREE.Geometry() );
}
if ( mesh.geometry.isBufferGeometry) {
var board = new THREE.Mesh( new THREE.BufferGeometry() );
}
i1 ++; // starts with -1 + 1 = 0
if ( i1 === 10 ) {i1 = 0; i10 ++ }
if ( i10 === 10 ) {i10 = 0; i100 ++ }
if ( i100 === 10 ) {i100 = 0 } // hundreds (reset when overflow)
if ( i100 > 0 ) {
d100 = digit[ i100 ].clone(); // digit for hundreds
board.add( d100 ); // on the board ...
d100.position.x = -8 * 0.1 * size; // ... move slightly to the left
}
if ( ( i100 > 0 ) || ( ( i100 === 0 ) && ( i10 > 0 ) ) ) { // no preceding zeros tens
d10 = digit[ i10 ].clone(); // digit for tenth
board.add( d10 ); // on the board
}
d1 = digit[ i1 ].clone(); // digit
board.add( d1 ); // on the board ...
d1.position.x = 8 * 0.1 * size; // ... move slightly to the right
vertexNumbers.push( board ); // place the table in the numbering data field
mesh.add( vertexNumbers[ i ] );
}
this.update = function ( ) {
if ( mesh.geometry.isGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set( mesh.geometry.vertices[ n ].x, mesh.geometry.vertices[ n ].y, mesh.geometry.vertices[ n ].z );
vertexNumbers[ n ].lookAt( camera.position );
}
}
if ( mesh.geometry.isBufferGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set(vertices[ 3 * n ], vertices[ 3 * n + 1 ], vertices[ 3 * n + 2 ] );
vertexNumbers[ n ].lookAt( camera.position );
}
}
}
}
|
| | | | | | |
| | 
HofK | Der Äquator wurde überschritten.
Allerdings recht unkonventionell.
Nachdem es vom Südpol zum Äquator geht, kommt der große Sprung  zum Nordpol. Von da geht es wieder zum Äquator. zum Nordpol. Von da geht es wieder zum Äquator.
Der Vorteil dabei ist der identische Algorithmus mit einem entsprechendem Offset. Auch konnte so die Kugelzone leicht über den Äquator ausgedehnt werden. Zusätzlich war eine Spaltung in Halbkugeln mit wählbarem Abstand sehr leicht möglich.
Weil ich dort [...]  geschrieben habe, dass Halbkugeln unterscheidbar sind, geschrieben habe, dass Halbkugeln unterscheidbar sind,
"I could possibly still think hemispheres as clearly distinguishable?"
gibt es das Beispiel mit zwei unterschiedlichen Texturen.

Allerdings erstmal nur bei BufferGeometry. Ich kann langsam verstehen, warum man sich auf eine Art konzentrieren möchte. Die Differenzen zwischen den Geometry Arten sind doch erheblich und man muss immer wieder neu denken. Beim uv-Mapping war hier BufferGeometry sehr einfach hinzuzufügen.
Wer sich mal versuchen möchte, kann probieren es für Geometry zu ergänzen und hier zu posten bevor ich dazu gekommen bin. Dann wird aus dem Monolog eventuell mal ein Dialog. 
'use strict'
var scene = new THREE.Scene();
var camera = new THREE.PerspectiveCamera(45,160/ 90 , 0.1, 100000);
camera.position.set(0,0,250);
var renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth,window.innerHeight);
renderer.setClearColor(0xcccccc);
document.body.appendChild(renderer.domElement);
THREEx.WindowResize(renderer, camera);
var controls = new THREE.OrbitControls( camera, renderer.domElement );
var clock = new THREE.Clock( true );
var time;
var g;
var sphere;
var radius;
var equatorGap; // proportionate to the radius
var bottomCircle, equator, topCircle;
var parts // radial parts
var verticesSum;
var vertexCount;
var vertexNorthOffset;
var faceCount;
var faceNorthOffset;
var x, y, z, ux, uy;
var a, b, c;
var ni, nji; // relative i, j
var Alpha;
var sinAlpha;
var cosAlpha;
var vertexNumbersHelperSphere;
var vertices; // for BufferGeometry / Helper
var vertexNormalsHelper;
var faceIndices;
var normals;
var uvs;
const SOUTH = -1;
const NORTH = 1;
var showGeo = false;
// material
var uvTex = new THREE.TextureLoader().load( "uvgrid01.png" );
var waterlilyTex = new THREE.TextureLoader().load( "waterlily.png" );
var side = THREE.DoubleSide;
var materials = [
new THREE.MeshBasicMaterial( { map: uvTex, wireframe: false, side: side } ), // uv grid
new THREE.MeshBasicMaterial( { map: waterlilyTex, side: side } ), // photo waterlily (free)
// new THREE.MeshBasicMaterial( { map: uvTex, side: side } ), // uv grid TEST
new THREE.MeshBasicMaterial( { transparent: true, opacity: 0.15, side: side } ), // transparent
new THREE.MeshPhongMaterial( { color: 0xff0000, emissive: 0xff0000, side: side } ), // red
];
var material = new THREE.MeshBasicMaterial( { color: 0x551155, side: THREE.DoubleSide, wireframe: false } );
document.getElementById( "show" ).onclick = showNewSphere;
animate();
//..............
function showNewSphere() {
if ( sphere ) {
if ( vertexNumbersHelperSphere ) sphere.remove( vertexNumbersHelperSphere );
scene.remove( sphere);
g.dispose();
showGeo = false;
}
// Geometry or BufferGeometry
if ( document.getElementById( "Geometry" ).checked ) g = new THREE.Geometry();
if ( document.getElementById( "BufferGeometry" ).checked ) g = new THREE.BufferGeometry();
radius = 50;
equatorGap = document.getElementById( "equatorGap" ).value; // * radius
parts = Math.floor( document.getElementById( "parts" ).value );
bottomCircle = Math.floor( document.getElementById( "bottomCircle" ).value );
topCircle = Math.floor( document.getElementById( "topCircle" ).value );
equator = Math.floor( document.getElementById( "equator" ).value );
vertexCount = 0;
if ( bottomCircle < equator ) {
for ( var i = bottomCircle; i <= Math.min( equator, topCircle ); i ++ ) {
vertexCount += i * parts;
}
vertexCount += bottomCircle === 0 ? 1 : 0; // south pole
}
vertexNorthOffset = vertexCount;
if ( topCircle > equator ) {
for ( var i = Math.max( equator, bottomCircle ); i <= topCircle; i ++ ) {
vertexCount += ( equator * 2 - i ) * parts ; // equator double (uv's)
}
vertexCount += topCircle === equator * 2 ? 1 : 0; // north pole
}
faceCount = 0;
for ( var i = bottomCircle; i < Math.min( equator, topCircle ); i ++ ) {
faceCount += ( 2 * i + 1 ) * parts;
}
if ( g.isBufferGeometry ) {
// write groups for multi material
for ( var f = 0, p = 0; f < faceCount ; f ++, p += 3 ) {
g.addGroup( p, 3, 0 ); // south: material 0
}
}
faceNorthOffset = faceCount ;
for ( var i = equator * 2 - topCircle; i < Math.min( equator, equator * 2 - bottomCircle ); i ++ ) {
faceCount += ( 2 * i + 1 ) * parts;
}
if ( g.isBufferGeometry ) {
for ( var f = faceNorthOffset , p = faceNorthOffset * 3; f < faceCount ; f ++, p += 3 ) {
g.addGroup( p, 3, 1 ); // north: material 1
}
}
if ( g.isGeometry ) {
for ( var i = 0; i < vertexCount; i ++ ) {
g.vertices.push( new THREE.Vector3( 0, 0, 0 ) );
}
}
if ( g.isBufferGeometry ) {
var idxCount = 0;
vertices = new Float32Array( vertexCount * 3 );
faceIndices = new Uint32Array( faceCount * 3 );
normals = new Float32Array( vertexCount * 3 );
uvs = new Float32Array( vertexCount * 2 );
g.setIndex( new THREE.BufferAttribute( faceIndices, 1 ) );
g.addAttribute( 'position', new THREE.BufferAttribute( vertices, 3 ).setDynamic( true ) );
g.addAttribute( 'normal', new THREE.BufferAttribute( normals, 3 ).setDynamic( true ) );
g.addAttribute( 'uv', new THREE.BufferAttribute( uvs, 2 ) );
var posIdx;
}
// faces south hemisphere
if ( bottomCircle < equator ) {
verticesSum = 0;
if ( bottomCircle === 0 ) {
a = 0; // vertex 0: south pole
b = 1;
c = 0;
for ( var j = 1; j <= parts; j ++ ) {
c ++;
b = c !== parts ? b + 1 : 1;
setFace(); // Geometry or BufferGeometry
}
verticesSum = 1; // only vertex 0, south pole
}
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i < Math.min( equator, topCircle ); i ++ ) {
for ( var p = 0; p < parts; p ++ ) {
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face in part
a = verticesSum;
b = a + parts * i + p + 1;
c = b - 1;
setFace(); // Geometry or BufferGeometry
} else {
// two faces / vertex
a = j + verticesSum;
b = a + parts * i + p;
c = a - 1;
if ( p === ( parts - 1 ) && j === i ) a -= parts * i; // connect to first vertex of circle
setFace(); // Geometry or BufferGeometry
// a from first face
b++; // b from first face
c = b - 1;
if ( p === ( parts - 1 ) && j === i ) b -= parts * ( i + 1 ); // connect to first vertex of next circle
setFace(); // Geometry or BufferGeometry
}
}
verticesSum += i;
}
}
}
// faces north hemisphere
if ( topCircle > equator ) {
verticesSum = vertexNorthOffset;
if ( topCircle === equator * 2 ) {
a = vertexNorthOffset; // vertex 0 + north offset: north pole
b = vertexNorthOffset;
c = 1 + vertexNorthOffset;
for ( var j = 1; j <= parts; j ++ ) {
b ++;
c = j !== parts ? c + 1 : 1 + vertexNorthOffset;
setFace(); // Geometry or BufferGeometry
}
verticesSum = 1 + vertexNorthOffset; // only vertex 0 + vertexNorthOffset
}
for ( var i = topCircle === equator * 2 ? 1 : equator * 2 - topCircle; i < Math.min( equator, equator * 2 - bottomCircle ); i ++ ) {
for ( var p = 0; p < parts; p ++ ) {
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face in part
a = verticesSum;
b = a + parts * i + p;
c = b + 1;
setFace(); // Geometry or BufferGeometry
} else {
// two faces / vertex
a = j + verticesSum;
b = a - 1;
c = a + parts * i + p;
if ( p === ( parts - 1 ) && j === i ) a -= parts * i; // connect to first vertex of circle
setFace(); // Geometry or BufferGeometry
// a from first face
b = c; // from first face
c = b + 1;
if ( p === ( parts - 1 ) && j === i ) c -= parts * ( i + 1 ); // connect to first vertex of next circle
setFace(); // Geometry or BufferGeometry
}
}
verticesSum += i;
}
}
}
// vertex positions south hemisphere
if ( bottomCircle < equator ) {
verticesSum = 0;
if ( bottomCircle === 0 ) {
if ( g.isGeometry ) g.vertices[ 0 ].set( 0, -radius - equatorGap / 2 * radius , 0 ); // south pole
if ( g.isBufferGeometry ) {
vertices[ 0 ] = 0;
vertices[ 1 ] = -radius - equatorGap / 2 * radius;
vertices[ 2 ] = 0;
uvs[ 0 ] = 0.5;
uvs[ 1 ] = 0.5;
}
verticesSum = 1; // only vertex 0, south pole
}
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i <= Math.min( equator, topCircle ); i ++ ) {
setVertex( SOUTH, equatorGap );
setUVs( SOUTH ); // only BufferGeometry
verticesSum += i * parts;
}
}
// vertex positions north hemisphere
if ( topCircle > equator ) {
verticesSum = vertexNorthOffset;
if ( topCircle === equator * 2 ) {
if ( g.isGeometry ) g.vertices[ vertexNorthOffset ].set( 0, radius + equatorGap / 2 * radius , 0 ); // north pole
if ( g.isBufferGeometry ) {
vertices[ vertexNorthOffset * 3 ] = 0;
vertices[ vertexNorthOffset * 3 + 1 ] = radius + equatorGap / 2 * radius ;
vertices[ vertexNorthOffset * 3 + 2 ] = 0;
uvs[ vertexNorthOffset * 2 ] = 0.5;
uvs[ vertexNorthOffset * 2 + 1 ] = 0.5;
}
verticesSum = 1 + vertexNorthOffset; // only vertex 0 + vertexNorthOffset, north pole
}
for ( var i = equator * 2 - topCircle; i <= Math.min( equator, equator * 2 - bottomCircle ); i ++ ) {
setVertex( NORTH, equatorGap );
setUVs( NORTH ); // only BufferGeometry
verticesSum += i * parts;
}
}
// g.computeVertexNormals;
// sphere = new THREE.Mesh( g, material );
sphere = new THREE.Mesh( g, materials ); // multi material array
if ( document.getElementById( "helper" ).checked ) {
vertexNumbersHelperSphere = new vertexNumbersHelper( sphere, 2.5, 0x3300ff);
vertexNumbersHelperSphere.update();
}
scene.add( sphere );
showGeo = true;
function setFace() {
if ( g.isGeometry ) {
g.faces.push( new THREE.Face3( a, b, c ) );
}
if ( g.isBufferGeometry ) {
faceIndices[ idxCount ] = a;
faceIndices[ idxCount + 1 ] = b;
faceIndices[ idxCount + 2 ] = c;
idxCount += 3;
}
}
// only BufferGeometry
function setUVs( south_north ) {
ni = i / equator; // rings;
for ( var j = 0; j < i * parts; j ++ ) {
nji = j / ( i * parts );
if ( g.isBufferGeometry ) {
if ( south_north === SOUTH ) {
ux = 0.5 * ( 1 + ni * Math.sin( 2 * Math.PI * nji ) );
uy = 0.5 * ( 1 + ni * Math.cos( 2 * Math.PI * nji ) );
}
if ( south_north === NORTH ) {
ux = 0.5 * ( 1 - ni * Math.sin( 2 * Math.PI * nji ) );
uy = 0.5 * ( 1 + ni * Math.cos( 2 * Math.PI * nji ) );
}
posIdx = ( verticesSum + j ) * 2;
uvs[ posIdx ] = ux;
uvs[ posIdx + 1 ] = uy;
}
}
}
function setVertex( south_north, equatorGap ) {
ni = i / equator; // rings;
Alpha = Math.PI / 2 * ni;
sinAlpha = Math.sin( Alpha );
cosAlpha = Math.cos( Alpha );
var gap = south_north === SOUTH ? -equatorGap / 2 * radius : equatorGap / 2 * radius;
for ( var j = 0; j < i * parts; j ++ ) {
nji = j / ( i * parts );
x = radius * sinAlpha * Math.cos( 2 * Math.PI * nji );
y = radius * cosAlpha * south_north + gap; // SOUTH -, NORTH +
z = - radius * sinAlpha * Math.sin( 2 * Math.PI * nji );
if ( g.isGeometry ) g.vertices[ verticesSum + j ].set( x, y, z );
if ( g.isBufferGeometry ) {
posIdx = ( verticesSum + j ) * 3;
vertices[ posIdx ] = x;
vertices[ posIdx + 1 ] = y;
vertices[ posIdx + 2 ] = z;
}
}
}
}
function animate(){
requestAnimationFrame(animate); // rekursiver Aufruf
time = clock.getElapsedTime();
if ( showGeo ) {
//sphere.rotation.x = 0.2 * time;
//sphere.rotation.y = 0.05 * time;
}
renderer.render(scene, camera);
}
function vertexNumbersHelper( mesh, size, color ) {
var vertexNumbers = [];
var materialDigits = new THREE.LineBasicMaterial( { color: color } );
var geometryDigit = [];
var digit = [];
var d100, d10, d1; // digits
var coordDigit = []; // design of the digits
coordDigit[ 0 ] = [ 0,0, 0,9, 6,9, 6,0, 0,0 ];
coordDigit[ 1 ] = [ 0,6, 3,9, 3,0 ];
coordDigit[ 2 ] = [ 0,9, 6,9, 6,6, 0,0, 6,0 ];
coordDigit[ 3 ] = [ 0,9, 6,9, 6,5, 3,5, 6,5, 6,0, 0,0 ];
coordDigit[ 4 ] = [ 0,9, 0,5, 6,5, 3,5, 3,6, 3,0 ];
coordDigit[ 5 ] = [ 6,9, 0,9, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 6 ] = [ 6,9, 0,9, 0,0, 6,0, 6,5, 0,5 ];
coordDigit[ 7 ] = [ 0,9, 6,9, 6,6, 0,0 ];
coordDigit[ 8 ] = [ 0,0, 0,9, 6,9, 6,5, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 9 ] = [ 6,5, 0,5, 0,9, 6,9, 6,0, 0,0 ];
if ( mesh.geometry.isGeometry) {
var verticesCount = mesh.geometry.vertices.length;
for ( var i = 0; i<10; i ++ ) {
geometryDigit[ i ] = new THREE.Geometry();
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
geometryDigit[ i ].vertices.push( new THREE.Vector3( 0.1 * size * coordDigit[ i ][ 2 * j ], 0.1 * size * coordDigit[ i ][ 2 * j + 1 ], 0 ) );
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
if ( mesh.geometry.isBufferGeometry) {
var verticesCount = vertices.length / 3 ;
var digitPositions = [];
for ( var i = 0; i < 10; i ++ ) {
geometryDigit[ i ] = new THREE.BufferGeometry();
digitPositions[ i ] = new Float32Array( coordDigit[ i ].length / 2 * 3 );
geometryDigit[ i ].addAttribute( 'position', new THREE.BufferAttribute( digitPositions[ i ], 3 ) );
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
digitPositions[ i ][ j * 3 ] = 0.1 * size * coordDigit[ i ][ 2 * j ];
digitPositions[ i ][ j * 3 + 1 ] = 0.1 * size * coordDigit[ i ][ 2 * j + 1 ];
digitPositions[ i ][ j * 3 + 2 ] = 0;
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
// numbering the vertices, hundreds ...
var i100 = 0;
var i10 = 0;
var i1 = -1;
for ( var i = 0; i < verticesCount ; i ++ ) {
// Number on board, up to three digits are pinned there
if ( mesh.geometry.isGeometry) {
var board = new THREE.Mesh( new THREE.Geometry() );
}
if ( mesh.geometry.isBufferGeometry) {
var board = new THREE.Mesh( new THREE.BufferGeometry() );
}
i1 ++; // starts with -1 + 1 = 0
if ( i1 === 10 ) {i1 = 0; i10 ++ }
if ( i10 === 10 ) {i10 = 0; i100 ++ }
if ( i100 === 10 ) {i100 = 0 } // hundreds (reset when overflow)
if ( i100 > 0 ) {
d100 = digit[ i100 ].clone(); // digit for hundreds
board.add( d100 ); // on the board ...
d100.position.x = -8 * 0.1 * size; // ... move slightly to the left
}
if ( ( i100 > 0 ) || ( ( i100 === 0 ) && ( i10 > 0 ) ) ) { // no preceding zeros tens
d10 = digit[ i10 ].clone(); // digit for tenth
board.add( d10 ); // on the board
}
d1 = digit[ i1 ].clone(); // digit
board.add( d1 ); // on the board ...
d1.position.x = 8 * 0.1 * size; // ... move slightly to the right
vertexNumbers.push( board ); // place the table in the numbering data field
mesh.add( vertexNumbers[ i ] );
}
this.update = function ( ) {
if ( mesh.geometry.isGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set( mesh.geometry.vertices[ n ].x, mesh.geometry.vertices[ n ].y, mesh.geometry.vertices[ n ].z );
vertexNumbers[ n ].lookAt( camera.position );
}
}
if ( mesh.geometry.isBufferGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set(vertices[ 3 * n ], vertices[ 3 * n + 1 ], vertices[ 3 * n + 2 ] );
vertexNumbers[ n ].lookAt( camera.position );
}
}
}
}
Die benötigten Scripte
three.min.86.js
OrbitControls.js
THREEx.WindowResize.js
kann man z.B. ganz einfach dort nach Strg+U anklicken. view-source: [...] 
und kopieren.
Da ist die Seerose [...]  und da das uv Grid [...] und da das uv Grid [...]  |
| | | | | | |
| | 
HofK | Genug der Vorbereitungen, jetzt wird es ernst mit der Ankündigung das Addon auf Polarkoordinaten / Kugelkoordinaten auszudehnen.
Schaut man da [...]  [...] [...]  , zeigt sich, dass es nicht genau eine Definition gibt. Auch ist die Anordnung der Koordinatenachsen bei three.js mit der z- Achse senkrecht zur Bildschirmebene zu beachten. , zeigt sich, dass es nicht genau eine Definition gibt. Auch ist die Anordnung der Koordinatenachsen bei three.js mit der z- Achse senkrecht zur Bildschirmebene zu beachten.
Deshalb benutze ich folgende Variante:
x = r * cos(theta) * cos(phi)
y = r * sin(theta)
z = r * cos(theta) * sin(phi)
Dabei läuft phi von der x-Achse gegen den Uhrzeigersinn um die y-Achse ( 0 bis 2*PI) und entspricht dem Verlauf der radialen faces und theta geht von der Äquatorialebene zu den Polen (0 bis PI/2 ). Dabei wird das Vorzeichen Minus für die südliche Halbkugel genutzt.
Da erhebliche Unterschiede bestehen und die Datei auch zu groß wäre, gibt es ein "neues" Addon THREEp.js.
Dazu habe ich THREEf.js "entkernt", nur die Hülle stehen lassen und fülle sie nun schrittweise aus.
Zunächst gibt es nur die Funktion g.rPhiTheta = function( u, v, t ) { return ... }; um den Radius abhängig von den Winkeln zu verändern. Sie entspricht dem bisherigen g.rCircHeight =function ( u, v, t ) { return ... };
Die Äguatorspalte ist bereits (noch fest) mit dabei, sie ist für Tests recht wichtig.
// geometry
var parameters = {
radius:50,
wedges:12,
equator:18,
rPhiTheta: function( u, v, t ) { return (u - 0.5) * (u - 0.5) + 0.8 + Math.sin( 1.57 * v) };
}


Die Funktion um die vertices zu positionieren:
function setVertex( south_north, equatorGap ) {
ni = i / eq;
theta = Math.PI / 2 * ( 1 - ni );
var gap = south_north === SOUTH ? -equatorGap / 2 * r : equatorGap / 2 * r;
for ( var j = 0; j < i * we; j ++ ) {
nji = j / ( i * we );
phi = 2 * Math.PI * nji;
r = g.radius * g.rPhiTheta( nji, ni );
x = r * Math.cos( theta ) * Math.cos( phi );
y = r * Math.sin( theta ) * south_north + gap; // SOUTH -, NORTH +
z = r * Math.cos( theta ) * Math.sin( phi );
posIdx = ( verticesSum + j ) * 3;
g.vertices[ posIdx ] = x;
g.vertices[ posIdx + 1 ] = y;
g.vertices[ posIdx + 2 ] = z;
}
}
Bei diesem Verfahren sind Südhälfte und Nordhälfte immer symmetrisch. Das gefällt mir nicht  - muss noch geändert werden. - muss noch geändert werden. |
| | | | | | |
| | 
HofK | HofK (11.08.2017)
Bei diesem Verfahren sind Südhälfte und Nordhälfte immer symmetrisch. Das gefällt mir nicht  - muss noch geändert werden.
War nicht so schwer 

g.rPhiTheta = function( u, v, t ) { return ( Math.sin( u )+ Math.sqrt( 0.2 + v ) * Math.sin( 3.14 * v * v) ) };
Einige kleinere Änderungen in der Funktion bringen es.
function setVertex( south_north, equatorGap ) {
ni = i / eq; // identically for south and north hemisphere: 0 pole to 1 equator
theta = Math.PI / 2 * ( 1 - ni ) * south_north; // SOUTH (-) NORTH (+)
gap = south_north * equatorGap / 2 * r;
ni = south_north === SOUTH ? ni / 2 : 0.5 + ( 1 - ni ) / 2; // 0 to 1 for sphere: g.rPhiTheta()
for ( var j = 0; j < i * we; j ++ ) {
nji = j / ( i * we );
phi = 2 * Math.PI * nji;
r = g.radius * g.rPhiTheta( nji, ni );
x = r * Math.cos( theta ) * Math.cos( phi );
y = r * Math.sin( theta ) + gap;
z = r * Math.cos( theta ) * Math.sin( phi );
posIdx = ( verticesSum + j ) * 3;
g.vertices[ posIdx ] = x;
g.vertices[ posIdx + 1 ] = y;
g.vertices[ posIdx + 2 ] = z;
}
}
|
| | | | | | |
| | 
HofK | HofK (11.08.2017)
Genug der Vorbereitungen, jetzt wird es ernst mit der Ankündigung das Addon auf Polarkoordinaten / Kugelkoordinaten auszudehnen.
Die erste, minimale Version ist auf GitHub verfügbar.
Da geht noch nicht viel, begonnen habe ich mit indexed BufferGeometry.
Ein Beispiel ist auch dabei.

Im Beispiel sind mit // auskommentierte Funktionen.
// rPhiTheta: function( u, v, t ) { return 0.25 + u * u + Math.sqrt(Math.abs( u - 0.5 )) }, aktiviert ergibt ein Entchen - wenn man einen Schnabel dazufügt.

Die Funktion function vertexNumbersHelper( mesh, size, color ) habe ich von THREEf.js mit übernommen, damit man nicht beide Bibliotheken laden muss. |
| | | | | | |
| | 
HofK | Mit THREEp.js geht es voran, es lassen sich schon künstliche Zähne erzeugen.
rPhiTheta: function( u, v, t ) { return 1 / ( 1 + Math.exp( Math.sin( 6.28 * u ) + v ) ) },
stretchNorth:function ( u, v, t ) { return 0.6 },
stretchSouth:function ( u, v, t ) { return 2 + Math.cos( 6.28 * u ) + v * v * Math.sin( 6.28 * v ) },

___________________________________________________
Wenn ich mir jetzt mal einige Codezeile von THREEf ansehe (abgucken!) frage ich mich manchmal: wie kommt man ( ich ) denn auf so etwas.
Mag sein, dass einige Leser sich das auch denken?
Gerade habe ich ein schönes Beispiel, das die Sache entzaubert  und ganz banal macht. und ganz banal macht.
Zuerst war da noch recht einfach nachvollziehbar
(eqt: Äquator, wed wedge, Kugelkeil - anfänglich part genannt )
// count faces: south and north hemisphere
faceCount = 0;
for ( var i = g.bottomCircle; i < Math.min( eqt, g.topCircle ); i ++ ) {faceCount += ( 2 * i + 1 ) * wed;}
Dann kam die Möglichkeit hinzu, den Boden einer Kugelschicht zu schließen (g.withBottom). Dazu benötigt man einen Mittelpunkt, ähnlich wie der Pol bei einer kompletten (Halb)Kugel und die entsprechenden verbindenden faces.
Also muss man "hinzudenken":
faceCount += ( g.bottomCircle > 0 && g.bottomCircle < eqt && g.withBottom ) ? g.bottomCircle * wed : 0;
Daraus folgen dann weitere Ergänzungen. So wird unter
// faces, uvs south hemisphere
aus einfachem
if ( g.bottomCircle === 0 ) { ...
for ( var j = 1; j <= wed; j ++ ) { ...
nun
if ( g.bottomCircle === 0 || g.withBottom ) { ..
jMax = g.bottomCircle === 0 ? wed : ( g.bottomCircle < eqt ? g.bottomCircle * wed : ( eqt * 2 - g.bottomCircle ) * wed );
for ( var j = 1; j <= jMax; j ++ ) { ...
Das macht sicher auch etwas Mühe, es korrekt zu gestalten, ist in dem Schritt aber doch überschaubar.
ABER! Da kommen sicher noch einige "Nebenwirkungen" schrittweise hinzu und dann schaut man nach einiger Zeit auf ein scheinbar undurchschaubares Ergebnis was man doch selber fabriziert hat.
Jeden einzelnen "Gedanken" zu dokumentieren ist auch nicht immer sinnvoll / möglich.
Aber hier das Ergebnis: Kugelschicht mit Boden.
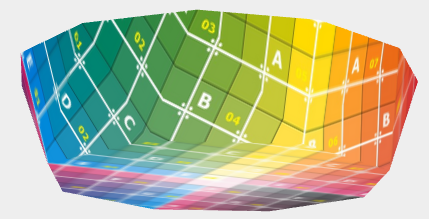
Version demnächst auf GitHub. |
| | | | | | |
| | 
HofK | HofK (17.08.2017)
Version demnächst auf GitHub.
demnächst ist JETZT!
Die noch etwas dürftige Version
- nur indexed BufferGeometry und wenige Eigenschaften / Funktionen -
ist dort [...]  zu finden. Dazu zwei Beispiele. zu finden. Dazu zwei Beispiele.
Das sieht auch ganz nett aus:
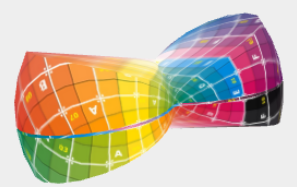
// geometry
var parameters = {
equatorGap: 0.05,
bottomCircle: 7,
withBottom: true,
topCircle: 12,
withTop: true,
rPhiTheta: function( u, v, t ) { return 1.5 + Math.sin( 4 * Math.PI * u ) },
} |
| | | | | | |
|
AntwortenThemenoptionen | 392.042 Betrachtungen |
ThemeninformationenDieses Thema hat 10 Teilnehmer: |