PHP, HTML & JavaScript- Forum | | | | | | - Seite 1 - |
| 
HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
| | | | | | |
| | | | | | - Seite 2 - |
| | Unterthema: Informationsinteresse 3D Grafik? [...]  erzeugt. |
| | | | | | |
| | 
HofK | Da zum 1. Advent hier im Flachland noch immer keine einzige Schneeflocke in Sicht ist, wollte ich mir unbedingt eine digitale Flocke gönnen.
Man braucht also ein Schneeflockenbild als Textur, kein Problem. In den (englischen) Foren geschaut, Quelltext vereinfacht übernommen. Keine Schneeflocke in Sicht aber Chrome gibt eine Fehlermeldung:
Bis fast zur Verzweiflung gesucht und die wildesten Sachen ausprobiert, bis ich zufällig statt dem sonst für three.js bevorzugtem Chrome mehr aus Versehen Firefox erwischt habe: da kam die Schneeflocke!
Etwas recherchiert. Es liegt wohl an den unterschiedlichen Sicherheitsstandards der Browser, Einheitlichkeit wäre ja auch zu langweilig für den Normalanwender.
Nur Firefox erlaubt laden der lokalen Datei (Schneeflocke), auch bei Opera ist keine Flocke in Sicht. Die Fehlermeldung ist nur die Folge, da ohne die Textur die Maschen einfach nicht erzeugt werden!
Stellt man die Datei ins Netz und öffnet sie online mit den Browsern, kann man sich die Flocke in den verschiedensten Browsern in Bewegung ansehen. Sogar in edge, wenn man Zeit hat zu warten und die Ruckelei nicht stört! Hier wird die Datei ja vom Server geladen, das ist immer ok.
Irgendwie blöd, dass nicht alle Browser erkennen, dass auch das JavaScript lokal gespeichert und lokal geladen wird.
Aber seit ich das Speicherchaos von Android 4.4 ergründet habe und immer wieder versuche auch edge eine Chance zu geben, wundert mich eigentlich nichts mehr in Bezug auf die Programmierqualitäten bei den "Großen".
Da [...]  bzw. [...] bzw. [...]  kann man Wintergefühle erhaschen und den kompakten Quelltext beschauen. Eine offline-Variante ist hier eventuell verwirrend! kann man Wintergefühle erhaschen und den kompakten Quelltext beschauen. Eine offline-Variante ist hier eventuell verwirrend!
Der große Flockenwirbel ist schon in Arbeit! 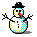
NACHTRAG:
Im Beispiel Androide [...]  wurde Revision 73 benutzt. Dort eine bereits in dieser Version als veraltet gekennzeichnete Verfahrensweise! wurde Revision 73 benutzt. Dort eine bereits in dieser Version als veraltet gekennzeichnete Verfahrensweise! |
| | | | | | |
| | 
HofK | Der große Flockenwirbel ist da.

30000 Schneeflocken je Schneeschauer fallen sanft. Die Technik dahinter nannte sich bei Three.js einmal Partikelsystem, nun heißt sie Punktesystem.
Das Problem ist, dass man bei der Suche fast ausschließlich auf etwas ältere Forenbeiträge bzw. Tutorials stößt. Diese nutzen die alte Variante.
Ich wollte aber unbedingt die aktuelle r82 benutzen! Welcher Begriff besser ist ? Es sind Punkte, die aber als Quadrat eine Größe haben (size) und eine Textur erhalten können. Es ist wie die Knoten eines Körpers ohne Kanten und Flächen. Es wird effektiv gerendert. Ich habe nicht versucht 30000 Schneeflocken als Körper (in einer Schleife ersteimal programmtechnisch kein Problem) zu erstellen um die Browser in die Knie gehen zu lassen.
Es ist wie immer wenn man weiß wie es geht, ganz einfach.
Seltsamerweise wird die Größe (size) im Material mit eingestellt.
// Schneeflocken (als System von Punkten)
pointCount = 30000; // Anzahl der Punkte (Schneeflocken)
points = new THREE.Geometry(); // eine allgemeine Geometrie fuer die Punkte erzeugen
var loader = new THREE.TextureLoader(); // ein Lader fuer die Textur
loader.load("schneeflocke.jpg", function(texture){ // Textur laden und damit gleich Punktesystem erzeugen
pointsMaterial = new THREE.PointsMaterial({ size: 21, color: 0xcccccc, map: texture, transparent: true, opacity: 0.95 });
for (var p = 0; p < pointCount; p++) { // zufaellige Koordinaten erzeugen
x = Math.random() * 4000 - 2000;
y = Math.random() * 2000 - 500;
z = Math.random() * 2000 - 2000;
point = new THREE.Vector3(x, y, z); // einzelnen Punkt erzeugen (als Ortsvektor seiner Koordinaten)
points.vertices.push(point); // Punkt als Knoten der Punkte-Geometrie hinzufuegen
}
// System der Punkte
pointSystem = new THREE.Points( points, pointsMaterial); // entsprechend THREE.Mesh bei Koerpern
// zur Szene hinzufuegen
scene.add(pointSystem);
pointSystem.rotation.x = 0.9;
});
Bei der Animation wird das Punktesystem zur Rotation gebracht und erzeugt so die Schneeschauer.
Da fällt der Schnee: [...]  bzw. [...] bzw. [...] 
Wie im vorherigen Beitrag bemerkt, ist eine offline-Variante hier nicht sehr sinnvoll. |
| | | | | | |
| | 
HofK | Noch einmal Knoten: --------- Besser als solche  Schleifen! Schleifen!
Weiter oben wurde die Nummerierung der Knoten mit einem zwar schicken, aber konstruktiv aufwändigem Rohrdesign realisiert. Der Browser muss sehr viele geometrische Objekte verkraften - das dauert oder zwingt manchen in die Knie!
Deshalb habe ich mal die Technik der Schneeflocke (Textur) zur Nummerierung benutzt. Die transparenten .png Dateien der Ziffern benötigen lediglich etwa 2KB. Die grundlegende Technik einer durchsichtigen Tafel ist fast identisch. Da aber immer lediglich Bilder angepinnt werden, ist die Rechenlast deutlich geringer. Deshalb gleich drei Körper.
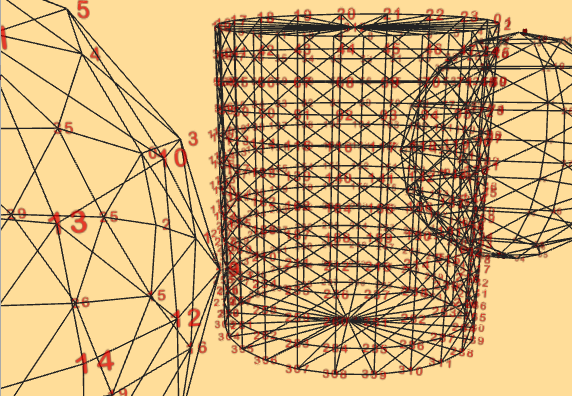
Auch die Ausrichtung zur Kamera in der xz Ebene ist wie oben realisiert.
Da [...]  bzw. [...] bzw. [...]  kann man die Sache ergründen. kann man die Sache ergründen.
Interessant, dass bei der THREE.SphereGeometry (Kugel) die Pole und der Nullmeridian pro Knoten scheinbar mehrere Nummern besitzen. Zieht man eine solche Knotennumer mal wie eine Nase (siehe oben) heraus, stellt man fest, das die unterschiedlichen Knoten nur auf einer Position liegen.
Damit kann man dann interessante Sachen machen, z.B. die Kugel auffalten.
Die Idee, die Nummerierung in selber Verfahrensweise mit einfachen 2D Sprites je Ziffer zu erledigen, funktioniert nicht. Diese Sprites richten sich dann einzeln automatisch immer zur Kamera aus. Schaut man von hinten, dreht sich z.B. 109 zu 901 - falsch.
Die in obigem Knotenbeitrag angesprochene Quelle [...] 
basiert auf der alten Revision 60 und erstellt recht kompliziert nur EIN Sprite für die komplette Zahl! |
| | | | | | |
| | 
HofK | Bald geht es daran den Weihnachtsbaum zu schmücken.
Da habe ich mal einige effektive Methoden ausprobiert - zumindest 3D virtuell.
Einfach eine Weihnachtsbaumkugelkette richtig in Schwung bringen und über den Baum werfen. Wenn sie dann austrudelt, ist der Baum schick.

Der Kern der Sache ist ein Punktesystem aus 600 Punkten. Diese werden in der Animation auf einer Spirale angeordnet. Die Punkte bewegen sich langsamer werdend auf der Spirale. Nach einiger Zeit, wenn die Frequenz recht klein ist, wird die Bewegung gestoppt. Die Kette hängt am Baum - fertig.
AUSZUG: JavaScript
// Punktesystem
anzahlPunkte = 600;
pointsGeometry = new THREE.Geometry();
for (var i = 0; i < anzahlPunkte ; i++)
pointsGeometry.vertices.push( new THREE.Vector3(0,0,0) ); // ersteinmal alle Punkte im Ursprung
texture = THREE.ImageUtils.loadTexture( 'redball.png' );
pointsMaterial = new THREE.PointsMaterial({color: 0xeee8aa, size: 50, map: texture, transparent: true, opacity: 0.7 , alphaTest: 0.5});
var pointSystem = new THREE.Points( pointsGeometry, pointsMaterial );
pointSystem.position.set(0, 85, 0);
scene.add( pointSystem );
function spirale(a,f,t) {
return new THREE.Vector3( a*f*t*Math.cos(f*t), 700-2*t, a*f*t*Math.sin(f*t) ); // x, y, z
}
function animate() {
requestAnimationFrame( animate );
controls.update();
t = clock.getElapsedTime();
f = 1.8 - Math.atan(0.5+t);
if (f>0.25){
for( var v = 0; v < pointsGeometry.vertices.length; v++ ) {
pointsGeometry.vertices[v] = spirale(2, f, t + 1.2*v); // neue Koordinaten jedes einzelnen Punktes (v)
}
pointsGeometry.verticesNeedUpdate = true; // zur Aktualisierung der Koordinaten der Punkte notwendig
}
camera.position.x = 1800*Math.sin(0.1*t);
renderer.render( scene, camera );
}
Detail:

Da [...]  bzw. [...] bzw. [...]  kann man es anschauen und den gesamten Quellcode einsehen. kann man es anschauen und den gesamten Quellcode einsehen.
Problem im normalen Leben:
Wie bekommt man die Kette derart in Schwung und ist dann genug Platz im Zimmer um den Baum herum.  |
| | | | | | |
| | 
HofK | Beim obigen Androiden Ring-Tennis habe ich die Wurf-und Stoß-Physik selbst in der Animation programmiert.
Zu three.js gibt es aber auch ein passendes Physik-Plugin. [...] 
Allerdings bezieht sich die letzte Änderung der Beispiele auf die Revision 73 von three.js vor etwa einem Jahr. Beim Versuch, Beispiele entsprechend selbst nachzuvollziehen erhielt ich immer wieder diverse Fehlermeldungen aus den Bibliotheken.
Die Verknüpfung von three.js und den weiteren Bibliotheken ist doch recht komplex. Die Versionen - wenn da ein Byte querliegt ...
Weiter gekramt, auch in der Röhre:
Da [...]  findet man die dafür benutzte Seite findet man die dafür benutzte Seite
"ICE code editor: [...]  " "
Dann findet man dort die three.js der Revision 52 vor. Dazu passend dann die benötigten Versionen der Bibliotheken:
physi.js
ammo.js
physijs_worker.js
Mit dieser älteren Version hat es dann auf Anhieb geklappt.
Mit etwa 250 JavaScript Zeilen ließ sich nun ein kleines, sicher noch unvollständiges Spiel bauen. Die Physik wird automatisch durch die Bibliotheken realisiert, in der Animation muss man nur die Abweichungen festlegen. Zum Beispiel, wenn der Ball von der Ebene fällt, soll er nicht unendlich tief fallen. Stattdessen muss er oder ein neuer Ball von oben herunterfallen.

Die physi.js schließt die Objekte/ Materialien von three.js in sich ein und erweitert sie um physikalische Eigenschaften. Diese werden dann intern berechnet und animiert.
Leider "hängt" die Physik in dieser Version zuweilen. Entweder noch Bugs in dieser Version, oder ich habe irgendeine notwendige Einstellung nicht gemacht - schwer herauszubekommmen.
Da [...]  bzw. [...] bzw. [...]  kann man das Spiel testen. kann man das Spiel testen.
Zum offline spielen komplett mit den zusammenpassenden 4 Bibliotheken gemeinsam in einem Ordner wo sie auch bleiben müssen:
Herunterladen
Da die Physik nicht ganz aktuell ist, belasse ich es erst einmal bei diesem kleinen Beispiel dazu.
Vom physi.js Autor gibt es noch eine weitere, nicht nur auf three.js fixierte JavaScript Physik: [...]  [...] [...]  |
| | | | | | |
| | 
HofK | THREEjs bietet eine Menge an vordefinierten geometrischen Objekten.
Um genauer zu schauen wie das funktioniert, ist es trotzdem angebracht, mal selber eine einfache eigene Konstruktion zu realisieren.
Dazu habe ich mit Blick auf Silvester in 14 Tagen ein Raketenleitwerk gebastelt. Es besteht lediglich aus drei an einem Punkt zusammenhängenden Flächen.

Die Öffnung ist variabel und wird animiert.
Die Geometrie-Objekte bestehen stets aus den Knoten (vertices) und den Flächen (faces). Dabei müssen komplexere Fächen immer in Dreiecke zerlegt werden, also sogar ein Rechteck durch seine Diagonale in zwei Dreiecke, da vier beliebige Punkte im Raum nicht unbedingt ein ebenes Viereck ergeben. In Beispielen weiter oben ist das gut sichtbar.
materialLeitwerk = new THREE.MeshNormalMaterial({ side: THREE.DoubleSide});
leitwerkGeometry = new THREE.Geometry(); // eine allgemeine Geometrie
leitwerkGeometry.vertices = [ // Datenfeld der Knoten, Koordinaten als Ortsvektoren, Index -> Flaechenbildung
new THREE.Vector3( 0, 10, 0 ), // Knoten 0 oben Mitte
new THREE.Vector3( 10, 0, 0 ), // Knoten 1 Spitze zu +x
new THREE.Vector3( 0, 0, -10 ), // Knoten 2 Spitze zu -z
new THREE.Vector3( -10, 0, 0 ), // Knoten 3 Spitze zu -x
new THREE.Vector3( 0, 0, 10 ), // Knoten 4 Spitze zu +z
new THREE.Vector3( 0, 0, 0 ), // Knoten 5 unten Mitte (alle 4 Knoten mit vorerst identischen Koordinaten)
new THREE.Vector3( 0, 0, 0 ), // Knoten 6 unten Mitte
new THREE.Vector3( 0, 0, 0 ), // Knoten 7 unten Mitte
new THREE.Vector3( 0, 0, 0 ), // Knoten 8 unten Mitte
];
//leitwerkGeometry.computeVertexNormals();
leitwerkGeometry.faces = [ // Datenfeld der Flaechen (Knotennummern der Ecken des Dreiecks in positivem Drehsinn)
new THREE.Face3( 0, 5, 1 ), // Leitflaeche zu +x
new THREE.Face3( 0, 6, 2 ), // Leitflaeche zu -z
new THREE.Face3( 0, 7, 3 ), // Leitflaeche zu -x
new THREE.Face3( 0, 8, 4 ) // Leitflaeche zu +z
];
leitwerkGeometry.computeFaceNormals(); // Berechnung der Normalen (Senkrechte Einheitsvektoren zur Flaeche -> MeshNormalMaterial)
leitwerk = new THREE.Mesh(leitwerkGeometry, materialLeitwerk);
scene.add(leitwerk);
Wie beim Pol der Kugel THREE.SphereGeometry habe ich mehrere Eckpunkte auf einen Koordinatenpunkt gelegt. Bei der Animation werden diese Koordinaten verändert.
Da [...]  bzw. [...] bzw. [...]  kann man die Animation und den kurzen Quelltext betrachten. kann man die Animation und den kurzen Quelltext betrachten. |
| | | | | | |
| | 
HofK | Ich wünsche allen Lesern des Themas
3D Grafik - WebGL mit three.js schöne weiße Weihnachten. 
Da das nicht jedes Jahr und überall klappt, habe ich ja vorgesorgt und wenigstens hier schon mal zum Advent den großen Flockenwirbel losgelassen.
Zu Weihnachten gibt es nicht nur Schnee, nein auch noch Geschenke!
Von mir und meinen kleinen Helfern gibt es liebevoll verpackt und unter den Baum geschoben eine exklusive, digital-virtuell gezüchtete Perle!

Da [...]  bzw. [...] bzw. [...]  liegt das Geschenk bereit. liegt das Geschenk bereit. 
Beim Weihnachtsgeschenk ist die Verpackung überaus wichtig. Selbst gebastelt kommt immer gut an.
Also ein Netz- und Flächenmodell für einen Würfel
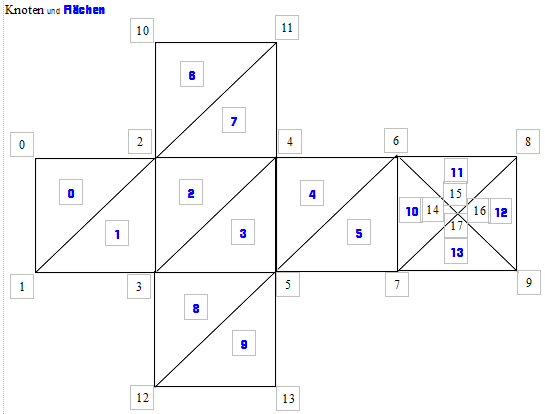
als Objekt erzeugt. Dazu alle Knoten mit ihren Koordinaten erzeugt.
// Paket basteln
paketGeo = new THREE.Geometry(); // eine allgemeine Geometrie
paketGeo.vertices = []; // Datenfeld der Knoten, Koordinaten als Ortsvektoren, Index -> Flaechenbildung
for(x=-30 ; x<51; x+=20){
paketGeo.vertices.push(new THREE.Vector3( x, 0,-10 )); // Knoten 0, 2, 4, 6, 8
paketGeo.vertices.push(new THREE.Vector3( x, 0, 10 )); // Knoten 1, 3, 5, 7, 9
}
paketGeo.vertices.push(new THREE.Vector3( -10, 0,-30 )); // Knoten 10
paketGeo.vertices.push(new THREE.Vector3( 10, 0,-30 )); // Knoten 11
paketGeo.vertices.push(new THREE.Vector3( -10, 0, 30 )); // Knoten 12
paketGeo.vertices.push(new THREE.Vector3( 10, 0, 30 )); // Knoten 13
paketGeo.vertices.push(new THREE.Vector3( 40, 0, 0 )); // Knoten 14 viermal identische Koordinaten
paketGeo.vertices.push(new THREE.Vector3( 40, 0, 0 )); // Knoten 15
paketGeo.vertices.push(new THREE.Vector3( 40, 0, 0 )); // Knoten 16
paketGeo.vertices.push(new THREE.Vector3( 40, 0, 0 )); // Knoten 17
paketGeo.computeVertexNormals();
Dann alle Flächen (immer Dreiecke!) durch die Knotennummern der Eckpunkte festlegen.
paketGeo.faces = [ // Datenfeld der Flaechen (Knotennummern der Ecken des Dreiecks in positivem Drehsinn von aussen)
new THREE.Face3( 0, 2, 1 ), // 0
new THREE.Face3( 1, 2, 3 ), // 1
new THREE.Face3( 2, 4, 3 ), // 2
new THREE.Face3( 3, 4, 5 ), // 3
new THREE.Face3( 4, 6, 5 ), // 4
new THREE.Face3( 5, 6, 7 ), // 5
new THREE.Face3( 10, 11, 2 ), // 6
new THREE.Face3( 2, 11, 4 ), // 7
new THREE.Face3( 3, 5, 12 ), // 8
new THREE.Face3( 12, 5, 13 ), // 9
new THREE.Face3( 14, 7, 6 ), // 10
new THREE.Face3( 15, 6, 8 ), // 11
new THREE.Face3( 16, 8, 9 ), // 12
new THREE.Face3( 17, 9, 7 ) // 13
];
paketGeo.computeFaceNormals(); // Berechnung der Normalen (Senkrechte Einheitsvektoren zur Flaeche -> Material)
Die Faltung des Würfels geschieht nun ganz einfach durch passende Änderung der Koordinaten der Knoten in der Animation,
z.B. bringt geo.vertices[0].y = geo.vertices[1].y = 20*Math.sin( w ); in der Funktion die zwei Knoten 0 und 1 schön langsam von 0 auf 20 hoch.
Die Animation hat zeitgesteuert 13 Phasen. Dabei wird für die Winkelfunktionen immer ein Viertelkreis, (1.57rad = 90°) je Phase erzeugt.
Interessant ist nun, was die Browser daraus machen. Zum debuggen habe ich die Anzahl der rekursiven Aufrufe ausgegeben. Wenn der Schneemann das Paket unter den Baum schiebt, ging das in meiner Firefox-offline von der RAM-Disk Arbeitsumgebung gemächlich in ca. 230 Tippelschritten knapp unter den Baum, online dann wechselnd mal nur 210. Bei Chrome und Opera geht es rasant mit ca.315 Schritten ab und das Paket knallt gegen den Baumstamm! [...] 
Bei "kleinweich" edge schafft es vorher die Perle nicht einmal in das Paket und die Sachen liegen dann wild herum! Da sind es nur ca. 140. Erstaunlich: IE 11 packt es wie Chrome und Opera. Was machen die da?
Auf meinem 4 Jahre alten Samsung Note 2 bringt mobiles Chrome erst 119 dann mal 150, beim Note 10.1 knallt das Paket gegen den Stamm.
Fazit:
Eine so einfach zeitgesteuerte Animation ist nicht praktikabel, es muss weg-zeitabhängig realisiert werden. |
| | | | | | |
| | 
Michael
W. | Cool, gleichfalls ein frohes Weihnachtsfest.   |
| | | | | | |
| | 
HofK | Kleidet man einen Würfel innen mit sechs zusammenhängenden Bildern als Textur aus und setzt die Kamera und eine (bewegliche) Linse in den Würfel, kann man die Lichtbrechung simulieren.

Da man solche Rundumbilder kaum selbst aufnehmen kann, habe ich auf frei verfügbare zurückgegriffen:
Textur (Bilder) von Emil Persson: [...] 
Creative Commons Lizenz Attribution 3.0
In einem recht neuen Buch von David J. Eck (Anfang 2016, free download, [...]  ) ist im Kapitel 5 Abschnitt 3 beschrieben, wie es gemacht wird. Dort auch der Link zu den Bildern. ) ist im Kapitel 5 Abschnitt 3 beschrieben, wie es gemacht wird. Dort auch der Link zu den Bildern.
Allerdings ist das Demo Beispiel im Buch wie meistens bei den three.js Beispielen so überfrachtet, dass der Anfänger Probleme bekommt den wesentlichen Punkt für sich richtig zu nutzen.
Deshalb habe ich radikal abgespeckt.
Andererseits gibt es in der Demo zwar mehrere einfache (nicht bewegliche) Grundkörper, aber keine Linse.
In einer anderen Demo im Buch wird gezeigt, wie Drehkörper erstellt werden. Nachdem ich den Demos des Buches die Revisionen 82 und die brandneue 83 untergeschoben hatte, funktionierten aber einige Beispiele wie gewohnt nicht. Darunter auch der Drehkörper.
Das hat auch anderen Leuten schon Probleme bereitet. Ein schönes Schachspiel wurde geschreddert, Bilder siehe: [...] 
Die Rotation erfolgt in den neueren Revisionen um eine andere Achse und statt eines dreikomponentigen Vektors wird nun einer mit nur zwei Werten erwartet. Es gibt aber keinen Fehler. Das Ergebnis des alten Codes ist nur "eigen".
Schaut man in der Referenz nach [...]  wird es klar: wird es klar:
"The lathe rotate around the Y axis. ...
LatheGeometry(points, segments, phiStart, phiLength)
points — Array of Vector2s. The x-coordinate of each point must be greater than zero."
Die Linse besteht aus zwei zur x-Achse symmetrischen Teilen eines Kreisbogens.
Problem: Da x>0 vorgegeben, gibt es nach der Rotation in der Mitte ein winziges Loch. Der Versuch es mit Werten wie 0.00001 auszutricksen war nicht erfolgreich.
Die wichtigsten Codepassagen:
Bildbox
//Bildboxtextur aus 6 Bildern, zusammenpassend an den Kanten, die Reihenfolge im Datenfeld ist wichtig!
var textureURLs = [];
textureURLs.push( "cubemap-textures/NissiBeach2/posx.jpg" );
textureURLs.push( "cubemap-textures/NissiBeach2/negx.jpg" );
textureURLs.push( "cubemap-textures/NissiBeach2/posy.jpg" );
textureURLs.push( "cubemap-textures/NissiBeach2/negy.jpg" );
textureURLs.push( "cubemap-textures/NissiBeach2/posz.jpg" );
textureURLs.push( "cubemap-textures/NissiBeach2/negz.jpg" );
// Textur - Material
skyboxTexture = THREE.ImageUtils.loadTextureCube( textureURLs, THREE.CubeRefractionMapping, render );
shader = THREE.ShaderLib[ "cube" ]; // enthaelt die benoetigten Shader
shader.uniforms[ "tCube" ].value = skyboxTexture; // Daten fuer die Shader
shMaterial = new THREE.ShaderMaterial( {
fragmentShader: shader.fragmentShader, // ShaderMaterial nimmt die benutzerdefinierten Vertex und Fragment Shader
vertexShader: shader.vertexShader,
uniforms: shader.uniforms, // Die Texture ist Teil dieses Objekts
//depthWrite: false,
side: THREE.BackSide // Rueckseite, d.h. Innenseite der Box
} );
// Bildbox ("Himmel")
skybox = new THREE.Mesh( new THREE.BoxGeometry( 100,100, 100), shMaterial );
scene.add(skybox);
Linse
//Linse
var points = []; // Punkte der x-y Ebene, die um die y- Achse rotiert werden
for ( var w = Math.PI; w > 1; w -= 0.02 ) {
if ( 2*Math.sin( w ) -1.8 >0 ) points.push( new THREE.Vector2( 2*Math.cos(w), 2*Math.sin(w)-1.8 )); // Vector2(x, y)
}
for ( var w = 1; w < Math.PI; w += 0.02 ) {
if ( 2*Math.sin( w ) -1.8 >0 ) points.push( new THREE.Vector2( 2*Math.cos(w), -(2*Math.sin(w)-1.8) )); //Vector2(x, y)
}
var geometry = new THREE.LatheGeometry( points, 32 ); // Drehteil (Drehung um y-Achse in Revision 83)
refMaterial = new THREE.MeshBasicMaterial({color: 0xffffff, envMap: skyboxTexture, refractionRatio: 0.8, wireframe:false} );
// Refraction (Lichtbrechung) zwischen 0 und 1.
// Default fast 1 - nahezu unsichtbares Glas.
refMaterial.reflectivity = 0.99; // durchgelassener Lichtanteil: 0 undurchsichtig, 1 voll durchlaessig
lens = new THREE.Mesh(geometry, refMaterial);
scene.add(lens);
lens.rotation.x = 1.57;
Da kann man durch die Linse schauen: [...]  sie auch bewegen und den knappen Quellcode sowie die Einzelbilder betrachten. sie auch bewegen und den knappen Quellcode sowie die Einzelbilder betrachten. |
| | | | | | |
| | 
HofK | Fertige Fotos als Textur wie im vorigen Beispiel sind recht bequem.
Wie geht das aber mit selbst erstellten Texturen? Dazu muss man sich mit der Frage beschäftigen, wie die Grafik auf den Bildschirm kommt. Neben der CPU gibt es da noch die GPU (Graphic Processing Unit). Diese arbeitet massiv parallel und bringt so überaus schnell die richtigen Farben auf alle Punkte des Displays.

Neben three.js (JavaScript) braucht man dazu noch weitere Skripte. Diese werden in der Sprache GLSL (OpenGL Shading Language) für Shader geschrieben (der Sprache C ähnlich).
Ich habe versucht, die Sache möglichst übersichtlich mit three.js zu kombinieren:
//GLSL Code aus den Shader Scripts einbinden
vertexShaderCode = document.getElementById( 'vertexShader' ).textContent
fragmentShaderCode = document.getElementById( 'fragmentShader' ).textContent
... usw. ...
WIDTH = 1200;
HEIGHT = 800;
renderer.setSize(WIDTH,HEIGHT); // Zeichenflaeche
shaderUniforms = {
u_time: { type: "f", value: 1.0}, // "f" float
u_resolution: { type: "v2", value: new THREE.Vector2() },
u_mouse: { type: "v2", value: new THREE.Vector2() }
};
shaderUniforms.u_resolution.value.x = WIDTH; // = renderer.domElement.width; // Wert zum Shader geben
shaderUniforms.u_resolution.value.y = HEIGHT; // = renderer.domElement.height; // Wert zum Shader geben
// Material aus dem Shader bilden
shMaterial = new THREE.ShaderMaterial( {
uniforms: shaderUniforms,
vertexShader: vertexShaderCode,
fragmentShader: fragmentShaderCode
} );
Uniforms sind die Variablen, die für alle Punkte der Zeichenfläche gelten, Kennung hier mit u_ .
Das erste Beispiel, eine komplett gelbe Fläche, ist im Ergebnis langweilig, dafür wird der Grundaufbau gut sichtbar und die GLSL Kommentare überwiegen im Skriptcode.
Einbindung der Skripte:
<script src="../js/three.min.83.js"></script>
<script id="vertexShader" type="x-shader/x-vertex">
// GLSL Code (OpenGL Shading Language)
void main() {
// Standardausgabe Position
gl_Position = vec4( position, 1.0 );// Position 3D, vierte Komp. > 1.0 Ausschnitt
}
</script>
<script id="fragmentShader" type="x-shader/x-fragment">
// GLSL Code (OpenGL Shading Language)
// uniform - Daten für alle ausgeführten GPU Threads einheitlich, nur lesbar, vgl. unten bei three.js
uniform vec2 u_resolution;// Groesse der Malfläche (canvas) in Pixeln (Breite, Hoehe)
uniform vec2 u_mouse;// Mausposition über der Malfleache in Pixeln (X, Y)
uniform float u_time;// Zeit in Sekunden seit dem Start des Bildaufbaus
//-----------------------------------------------------------
void main() {
// Die Verarbeitung erfolgt parallel in den Pipelines der GPU (Graphic Processing Unit)
// Standardeingabe Fragmentkoordinaten: gl_FragCoord (vordefiniert mit allen x,y Koordinaten)
// Standardausgabe Fragmentfarbe: gl_FragColor (vordefiniert Fragmentfarbe zu allen Koordinaten)
// Farbe (Farbkanäle Rot, Grün, Blau und Alpha) ergibt sich aus:
// Komponenten: 1 aus x Koordinate, 2 aus y Koordinate, 3 fix 0.0, 4 Deckkraft: 1.0
gl_FragColor = vec4(gl_FragCoord.xy, 0.0, 1.0);// Vektor mit 4 Komponenten
// alle Punkte des Fragments Gelb,
// da Koordinaten nicht kleiner 1 und Farbanteile 0.0 bis 1.0 erwartet (kein Fehler, >1 wie =1)
// Farbenspiele und Muster durch Berechnungen mit gl_FragColor,
// die einen vec4 mit Werten zwischen 0 und 1 ergeben.
}
</script>
Will man etwas mehr erreichen, muss man "nur" einige Berechnungen anstellen:
// normalisierte Koordinaten bilden - Achse x, y zwischen 0.0 und 1.0
// dazu: Fragment Koordinaten dividiert durch Auflösung der Zeichenfläche (je Achse!)
vec2 s = gl_FragCoord.xy / u_resolution.xy;// s hat die zwei Komponenten x und y
s *= 4.0;// Skalierung auf 0.0 bis 4.0 (je Achse)
s = fract(s);// fract (Nachkommastellen) --> ergibt 4 mal jeweils 0.0 bis 1.0 je Achse
// Farbkomponenten nach umgewandelten x,y Koordinaten, dritter Anteil schwankt mit Zeit:
vec3 c = vec3( s.x, s.y, abs(sin(u_time)) );
// Standardausgabe Fragmentfarbe: gl_FragColor (vordefiniert)
gl_FragColor = vec4( c, 1.0 );// parallele Ausgabe - Farbe mit Deckkraft: 1.0
Da [...]  kann man erste einfache Beispiele betrachten und den kommentierten Quellcode einsehen. kann man erste einfache Beispiele betrachten und den kommentierten Quellcode einsehen.
____________________________________________________________
Eine sehr gut verständliche Einführung [...]  dazu gibt es im Online Buch [...] dazu gibt es im Online Buch [...]  in mehreren Sprachen, auch Deutsch. Hier kann man auch unmittelbar die Beispiele verändern. Sogar, indem man mit der Maus per ein- oder zweidimensionalem Eingabebereich mit den Konstanten spielt. Das Ergebnis ist sofort sichtbar, z.B. auf der Seite [...] in mehreren Sprachen, auch Deutsch. Hier kann man auch unmittelbar die Beispiele verändern. Sogar, indem man mit der Maus per ein- oder zweidimensionalem Eingabebereich mit den Konstanten spielt. Das Ergebnis ist sofort sichtbar, z.B. auf der Seite [...]  . .
Spielen kann man auch in der Sandbox [...]  . .
Ganz einfach z.B [...]  aber auch sehr komplex aber auch sehr komplex
Delphin: [...] 
Weihnachtsbaum: [...] 
Wasser: [...] 
Apfel: [...]  |
| | | | | | |
| | 
Michael
W. | | | | | | | |
|
AntwortenThemenoptionen | 391.514 Betrachtungen |
ThemeninformationenDieses Thema hat 10 Teilnehmer: |