| |
| |
|
| - page 1 - |
|

HofK | sur une appeler  Tipp de IF hin, habe je mir la fois Tipp de IF hin, habe je mir la fois
three.js [...]  angeschaut. là [...] angeschaut. là [...]  (entier unten) qui ersten Resultate. (entier unten) qui ersten Resultate. |
|
| |
| |
| |
|
| |
| |
| - page 8 - |
|
|

HofK | qui qui Wahl hat, hat qui tourment!  
il y a so quelques Opportunités à qui Grundform Kugel herumzuwerkeln.
quoi soll on là prendre 
Pour Boden et le couvercle habe je probiert qui Kugelkeile trop schließen.
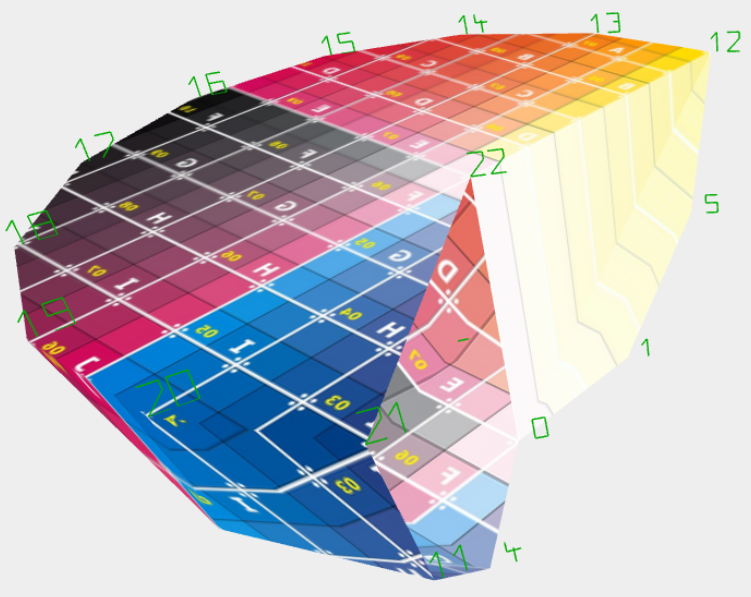
cela funktioniert sans grand Aufwand, si on qui faces avec den vorhandenen vertices bildet. là je vorerst avec indexed BufferGeometry arbeite, wird mais tout de suite cela Problem avec dem uv-Mapping deutlich. qui vertices avons bereits uv's et so ergibt sich qui Verzerrung qui Textur.
Beim Boden / le couvercle am Pol ist cela oui korrekt, comment on chez den Bildern qui letzten Posts erkennt. mais Boden / le couvercle comme Gegenstück zum Pol ergeben sur cet Art une spiegelbildliche Textur - im Bild trop erkennen. chez qui "abgewählten" Geometry hat on cela Problem pas, là qui uv's chez den faces gespeichert volonté.
chez BufferGeometry gibt es seulement vertex uv's. on muss alors alle betroffenen vertices chez selber situation - zeitabhängig dans morphVertices() - doppeln et avec cela qui neuen faces bilden. ensuite peux on sogar une eigene Textur aufbringen. veux on cela? un erheblicher Mehraufwand!
Dabei: pourquoi qui Geometry trotz aller Theorie et intention flotter ist, sais je toujours pas. [...]  [...] [...] 
mariage je mich entscheide, werde je seulement einmal regarder, comment je qui Kugel breitquetschen peux. comment chez THREEf unrollCover wird qui Radius sur dem qui verices liegen toujours größer, jusqu'à presque unendlich. ensuite gibt es ici si gleichmäßig gequetscht wird schließlich deux Kreise (Süd / Nord) avec dem Radius r * PI/2.
squeeze,// function ( v, t )// 0 sphere to 1 flat circle
cela funktioniert anders comme stretchSouth / stretchNorth
là wird seulement qui y Koordinate per verändertem Radius manipuliert.
function xyzCalculation( south_north, phi, theta, thetaY ) {
r = g.radius * g.rPhiTheta( nji, ni, t );
x = r * Math.cos( theta ) * Math.cos( phi ) + g.radius * g.moveX( nji, ni, t );
z = - r * Math.cos( theta ) * Math.sin( phi ) + g.radius * g.moveZ( nji, ni, t );
r *= ( south_north === SOUTH ? g.stretchSouth( nji, ni, t ) : g.stretchNorth( nji, ni, t ) ) ;
y = r * Math.sin( thetaY ) + south_north * gap + g.radius * g.moveY( nji, ni, t );
} |
|
| |
| |
| |
|
|

p.specht
 | | démence, quoi là alles allez! |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 25.08.2017 ▲ |
|
| |
|
|

HofK | |
| |
| |
| |
|
|

HofK | Pour einigen Fehlversuchen et Changements am vorhandenen Code ist eh bien THREEp.js ( rev 87.1 alpha ) sur GitHub [...]  et déjà chez [...] et déjà chez [...]  posté. posté.
Incidemment nutze je neuerdings deepl [...]  comme Übersetzungshilfe. pouvoir sich besser comme Google Translator. comme Übersetzungshilfe. pouvoir sich besser comme Google Translator.
cela habe je ( avec nachträglichen eigenen Anpassungen - qui Fachtermini sommes toujours un Problem) traduit:
THREEp.js. - une Avancé Alpha Version ist eh bien sur GitHub disponible.
- Es funktioniert avec three.js r87.
- qui Kugelkeile peut à qui page geschlossen volonté (default).
- qui Äquator Lücke ist eh bien comme Funktion disponible.
avec qui Äquator Lücke - eh bien comme Funktion - ouvrez et schließt un kleines Monster son la bouche. avec paramètre t - Zeit.
screenshots exampleA2.html
qui Bilder la fois seulement là: [...] 
var parameters = {
equator: 4,
equatorGap: function( u, t ) { return 0.5 *( 1 + Math.cos( 6.28 * u)) *( 0.5 - u )*( 0.5 - u ) * ( 1 + Math.sin( t ) ) },
stretchSouth: function ( u, v, t ) { return ( 1 + Math.cos( 6.28 * u)) *( 0.5 - u )*( 0.5 - u ) * ( 1 + Math.sin( t ) ) },
wedges: 11,
usedWedges: 8,
topCircle: 7,
withTop: vrai,
bottomCircle: 3,
withBottom: vrai,
}
|
|
| |
| |
| |
|
|

HofK | 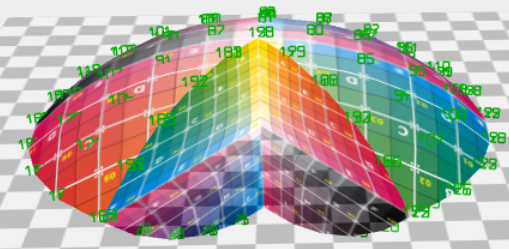
qui contusion mais est komplizierter, comme je mir cela so vorgestellt hatte:
simple draufdrücken  et fertig. et fertig.
c'est pourquoi habe je pour einigen Bleistift- Kritzeleien entier vers mon Art doch la fois une halbwegs saubere Skizze fabriziert:
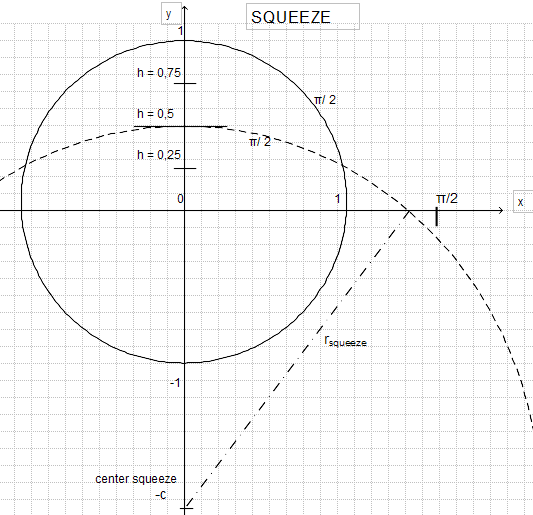
Beispielsweise sous [...]  findet on ausreichend viele Formeln zur Berechnung. findet on ausreichend viele Formeln zur Berechnung.
qui Bogen des Viertelkreises avec dem Radius 1 muss sur den Bogen des halben Kreissegments abgebildet volonté. qui Bogenlänge ist stets Pi/2.
Dabei ist qui partage qui Schnittpunkte sur qui x et y Achse pas proportional! Hat on qui Hauteur sur 0,5 gedrückt, ist qui halbe Sehne bereits sur deutlich plus que qui Moitié de 1 trop Pi/2 vorgerückt.
Beim Versuch, une Funktion pour qui dépendance trop ermitteln habe je très vite aufgegeben. Trigonometrische Gleichungen sommes pas toujours geschlossen lösbar. qui ermittelte Zusammenhang
cos( Pi / (2*r) ) = 1 - h/r, (r squeeze) um cela centre et den Winkel des grand Kreises trop bestimmen, machte wenig Mut.
Peut-être sous den Lesern un Trigonometrieexperte qui cela löst ou bien zeigt: pas lösbar?
c'est pourquoi verfolge je folgenden Ansatz:
je gebe une fiktive Quetschrate avant et ermittele daraus ensuite qui zugehörigen nécessaire Werte:
Aus h = r * ( 1 - cos (alpha / 2 ) ) avec r = (Pi/2) / alpha
peux on qui Hauteur et ensuite qui anderen Werte ermitteln. Dabei zeigt sich, dass Quetschrate (squeeze) et Hauteur etwa "zueinander passen". qSq = 1 - squeeze
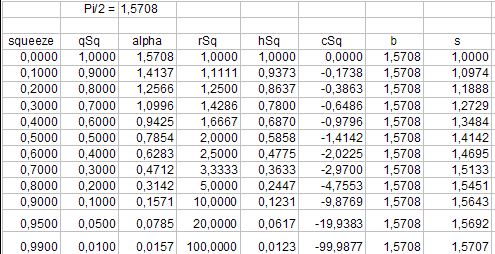
quelque chose schwieriger comme chez den Zylinderkoordinaten dans THREEf gestaltet sich aussi qui Mischung qui Funktionen. qui Winkel Theta wird par qui contusion modifié, ist mais Argument qui Funktionen.
qui encore pas optimierte mais funktionierende Code:
// ////// only squeeze //////////// ///////////////////////////////////////////////////
qSq = 1 - g.squeeze( t );
alphaSq = qSq * pi2; // squeeze angle
rSq = 1 / qSq; // radius squeeze circle
hSq = pi2 / alphaSq * ( 1 - Math.cos( alphaSq ) ); // height (squeezed)
cSq = rSq - hSq; // center(y)squeeze circle
/////////////////////////////////////////////////////////////////////////////////////////////
function xyzCalculation( south_north ) {
r0 = g.radius;
x0 = r0 * Math.cos( theta ) * Math.cos( phi );
y0 = r0 * Math.sin( thetaY );
z0 = -r0 * Math.cos( theta ) * Math.sin( phi );
r1 = g.radius * g.rPhiTheta( nji, ni, t );
r1y = r1 * ( south_north === SOUTH ? g.stretchSouth( nji, ni, t ) : g.stretchNorth( nji, ni, t ) );
x1 = r1 * Math.cos( theta ) * Math.cos( phi ) + g.radius * g.moveX( nji, ni, t );
y1 = r1y * Math.sin( thetaY ) + g.radius * ( south_north * g.equatorGap( nji, t ) / 2 + g.moveY( nji, ni, t ) );
z1 = - r1 * Math.cos( theta ) * Math.sin( phi ) + g.radius * g.moveZ( nji, ni, t );
dx = x1 - x0;
dy = y1 - y0;
dz = z1 - z0;
//------------
r2 = r0 * rSq;
thetaSq = south_north * ( pi2 - alphaSq ) + alphaSq * theta / pi2 ;
thetaSqY = south_north * ( pi2 - alphaSq ) + alphaSq * thetaY / pi2 ;
x2 = r2 * Math.cos( thetaSq ) * Math.cos( phi );
y2 = r2 * Math.sin( thetaSqY ) - south_north * r0 * cSq;
z2 = - r2 * Math.cos( thetaSq ) * Math.sin( phi );
// ------------
x = x2 + dx;
y = y2 + dy;
z = z2 + dz;
}
Schnappschüsse (Funktion avec t - Zeit):
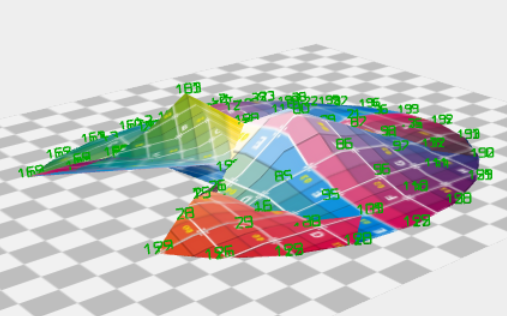
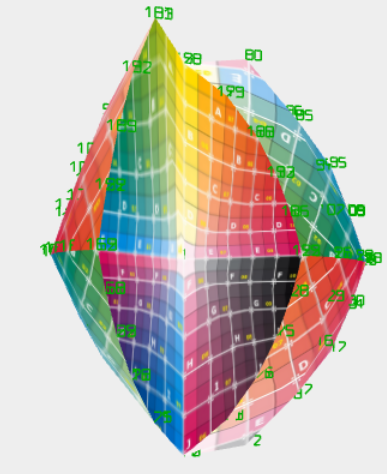
var parameters = {
equator: 5,
//squeeze: function( t ) { return 0.99}, // chez 1 encore FEHLER 1/0 - Radius UNENDLICH
squeeze: function( t ) { return 0.45 * ( 1 + Math.sin( 0.5 * t ) ) },
rPhiTheta: function ( u, v, t ) { return 0.75 + 2 * (0.5-v)*(0.5-v) + 0.2 * Math.sin( 6.28 * u) },
stretchNorth: function ( u, v, t ) { return 1 + 0.4 * u },
wedges: 5,
usedWedges: 4,
} |
|
| |
| |
| |
|
|

HofK | Im obigen Beispiel ist squeeze encore sur den paramètre t beschränkt. Bien sûr venez ici encore qui azimutale Winkel hinzu et qui contusion peux rundherum dosiert volonté.
deux Schnappschüsse avec einer Dahlie de qui IGA dans Berlin:


var parameters = {
squeeze: function ( u, t ) { return 0.45 * ( 1 + Math.sin( 6.28 * u ) * Math.sin( t ) ) },
equator: 8,
wedges: 6,
usedWedges: 5,
wedgeOpen: faux, // default is vrai now
}
là es par qui verschiedenen Funktionen aussi Sinn pouvoir chez wedges === usedWedges wedgeOpen trop nutzen, habe je cela inhaltlich geändert. |
|
| |
| |
| |
|
|

HofK | Um qui Neuerungen dans THREEp.js einfacher testen trop peut et um aussi cet Sandbox toujours halbwegs aktuell trop avons, startet qui Box maintenant dans qui alpha Phase.
en supplément habe je sur sandbox.threejs.hofk.de/ [...]  une Auswahlseite hochgeladen. une Auswahlseite hochgeladen.
de là venez on zur "alten" Sandbox THREEf et zur dans qui Entwicklung befindlichen Box pour THREEp.
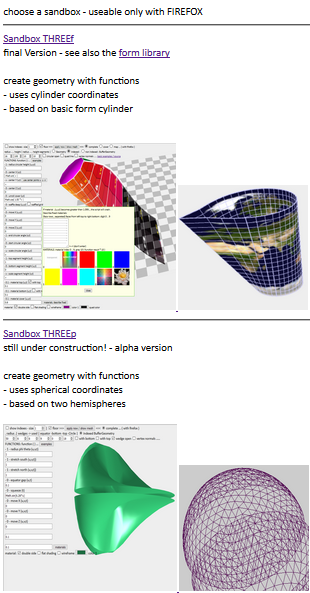
qui direckte Weg ist
sandboxthreef.threejs.hofk.de/ [...] 
ou
sandboxthreep.threejs.hofk.de/ [...] 
Beide Seiten marcher seulement avec Firefox.
 |
|
| |
| |
| |
|
|

HofK | eh bien funktioniert partiellement déjà Multimaterial.

var materials = [
// matériel index:
new THREE.MeshBasicMaterial( { transparent: vrai, opacity: 0.15, side: side } ),// 0 transparent
new THREE.MeshBasicMaterial( { map: uvTex, side: side } ),// 1 uv grid
new THREE.MeshPhongMaterial( { color: 0xff0000, emissive: 0xff0000, side: side, } ),// 2 red
new THREE.MeshPhongMaterial( { color: 0x00ff00, emissive: 0x00ff00, side: side, } ),// 3 green
new THREE.MeshPhongMaterial( { color: 0x0000ff, emissive: 0x0000ff, side: side, } ),// 4 blue
new THREE.MeshPhongMaterial( { color: 0xffff00, emissive: 0xffff00, side: side, } ),// 5 yellow
new THREE.MeshPhongMaterial( { color: 0xff00ff, emissive: 0xff00ff, side: side, } ),// 6 mgenta
new THREE.MeshPhongMaterial( { color: 0x00ffff, emissive: 0x00ffff, side: side, } ),// 7 cyan
new THREE.MeshBasicMaterial( { map: dahliaTex, side: side } ),// 8 photo dahlia (free)
new THREE.MeshPhongMaterial( { color: 0xee55ff, emissive: 0x7733dd, side: side } ),// 9 color
new THREE.MeshPhongMaterial( { color: 0x444444, emissive: 0x333333, side: side } )// 10 grey
];
var parameters = {
materialSouth: function ( u, v, t ) { return u },
materialNorth: function ( u, v, t ) { return v },
equator: 10,
wedges: 10,
}
là matériel 0 transparent ist, peux on dans qui Kugel, par qui Kugel hindurch regarder.
chez 10 Kugelkeilen bzw. Ringen jusqu'à zum Äquator volonté qui Materialien 0 jusqu'à 9 genutzt.
dans qui Sandbox [...]  peux on cela selber ausprobieren (Firefox). peux on cela selber ausprobieren (Firefox).
qui Materialspielerei erreicht on wieder par "passende" Indexrechnungen.
Dabei tomber qui Differenzen qui Quadrat comment i * i - g.bottomCircle * g.bottomCircle ins Auge. qui Quadrate sommes qui somme qui faces dans einem coin vom Pol beginnend, 1 + 3 + 5 + 7 ..., alors somme qui ungeraden payons. cela Ergebnis ist cela Quadrat qui Nombre de Summanden, ici alors 4*4 = 16.
|
|
| |
| |
| |
|
|

ByteAttack | Ist vraie qui marteau den Du là fais! si es so plus allez, bekommst Du ici encore deine eigene Wiki...  |
|
| |
| |
| |
|
|

HofK | un fieser Bug  hat mich genervt et Zeit gekostet. il était déjà länger drin. mais seulement chez certain Parameterkonstellationen wurde il sichtbar. So konnte il längere Zeit durchschlüpfen. hat mich genervt et Zeit gekostet. il était déjà länger drin. mais seulement chez certain Parameterkonstellationen wurde il sichtbar. So konnte il längere Zeit durchschlüpfen.
Es fehlten soudain faces! chez genauerer Betrachtung étions pour à identischer Position faces doppelt vorhanden.
là qui Code doch déjà quelque chose komplexer ist et qui Struktur komplizierter comme beim Zylinder, konnte Je l' faute pas trouver et habe quelques avec ähnlichen Fehlern behaftete Varianten produziert .
qui positive Nebeneffekt ist, dass qui Funktion vertexNumbersHelper eh bien sur vertexFaceNumbersHelper erweitert ist. facultativement vertices ou bien faces ou bien beide Dinge.
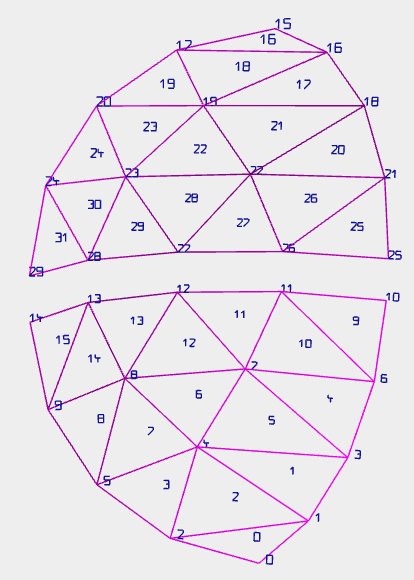
avec cette Aider hatte qui punaise  ensuite aucun chance plus. ensuite aucun chance plus.
Im Endeffekt était es une fehlerhafte Zählung dans qui Boucle pour qui wedges. seulement si Nord- et Südhalbkugel avec geschlossenem Kugelkeil gebildet wurden et qui Bodenkreis pas 0 était, trat qui faute im südlichen wedge sur et qui letzten faces qui Nordhalbkugel fehlten. cela matériel était ensuite faux zugeordnet. ici une qui produzierten Fehlleistungen:
faux

... mais richtig

sûrement encore pas correct - ALPHA - mais zum experimentieren approprié qui aktuelle Version là: [...]  (firefox) (firefox) |
|
| |
| |
| |
|
|

HofK | qui aucun Zeit ou bien Lust hat dans qui sandbox selber quelque chose auszuprobieren, peux maintenant là [...]  vite Video regarder. ne...aucune abendfüllendes Programme, mais toujours sur dem aktuellen Stand. toujours qui neuesten Kreationen! vite Video regarder. ne...aucune abendfüllendes Programme, mais toujours sur dem aktuellen Stand. toujours qui neuesten Kreationen!
...........................................................................
maintenant stehe je avant einer Designentscheidung.
et qui ist schwieriger comme vorhin beim Hecke schneiden - rund kurz ou bien plus dranlassen. qui nature wird es sowieso wieder croître lasssen. cela Softwaredesign ist là statischer!
cela Problem:
qui Skalierung des Azimuts (phi) bezieht sich entier naturellement sur beide Halbkugeln:
endAzimuth,//function ( v, t )// end azimuth angle phi (per theta)
startAzimuth,//function ( v, t )// starting azimuth angle phi (per theta)
scaleAzimuth,//function ( u, t )// scaling between start and end of azimuth angle ( phi 0 .. 2*PI)
Beim Polwinkel ist cela pas so bien sûr. interne wird chacun Halbkugel gesondert vom Pol zum Äquator berechnet. voudrais on maintenant vom Südpol zum Nordpol skalieren, gibt es une umfangreiche Unterscheidung comment chez qui Erstellung qui vertices et faces.
là ist cela ne...aucune Problem, là qui l'affaire seulement einmal fonctionnement wird. qui Skalierung muss mais ständig dans qui Funktion xyzCalculation( south_north ) zeitabhängig berechnet volonté.
chez stretch... habe je mich déjà pour deux gesonderte Funktionen pour qui Halbkugeln entschieden. qui plus dessus abgebildete "Zahn" zeigt, dass es durchaus Sinn pouvoir.
Momentan ist es so, dass qui Funktionen identique sur beide Halbkugeln wirken.
(Zählung pour Halbkugeln nih, - pour Kugel ni, - Vertices im Kreis i: nji; Äquator ist eqt )


bien am Netzwerk erkennbar qui Skalierung pour qui Wurzelfunktion.
qui Berechnung pour Nord -et Südpol et cela centre dans qui Mitte fehlt encore, c'est pourquoi pas korrekt!
Nimmt on deux getrennte Funktionssätze, muss qui Nutzer chez besoin cet so "auswählen", dass une gewünschte einheitliche Skalierung de Süd pour Nord entsteht. c'est wiederum préjudiciable weil quelque chose schwieriger comme avec einem Funktionssatz trop travailler.
je prends gern sachdienliche Hinweise entgegen!
 ........ ........ ----- ----- |
|
| |
| |
| |
|
|

HofK | qui Skalierung ist presque geschafft.
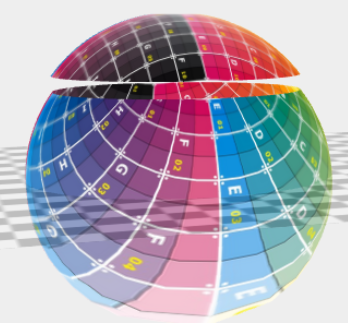
scalePole: function( v, t ) { return Math.sqrt( v ) },

scalePoleH: function( v, t ) { return Math.sqrt( v ) },
là je mich pas entscheiden konnte, est un Kompromiss qui beste Solution.
il peut une Funktion scalePoleHemisphere ou bien
scalePole angeben. interne wird avec deux Funktionen pour Süd et Nord gearbeitet. Dabei bedurfte es pas qui befürchteten Unterscheidung comment chez qui Erstellung qui Geometrie. une sinnvolle change suffisant!

qui Angabe de Funktion scalePole überschreibt une vorhandene Funktion scalePoleH. |
|
| |
| |
| |
|