PHP, HTML & JavaScript- Forum | | | | | | - page 1 - |
| 
HofK | sur une appeler  Tipp de IF hin, habe je mir la fois Tipp de IF hin, habe je mir la fois
three.js [...]  angeschaut. là [...] angeschaut. là [...]  (entier unten) qui ersten Resultate. (entier unten) qui ersten Resultate. |
| | | | | | |
| | | | | | - page 7 - |
| | 
HofK | afin de regarder, si qui Farbgestaltung Einfluss sur qui Geschwindigkeit nimmt, habe je encore qui Auswahlmöglichkeiten multicolor et monochrome hinzugefügt. chez monochrome volonté ensuite seulement encore qui vertices, manipuliert (forme), qui Farbgebung per
si ( multicolor ) { ... } ausgeblendet.

cela ändert mais rien am Ergebnis. [...]  |
| | | | | | |
| | 
HofK | après que THREEf.js ersteinmal soweit komplett ist, habe je la fois geschaut, comme dans direction Polarkoordinaten continuer pourrait.
en supplément nécessaire on une Kugel. dans three.js ist une Kugel (sphere) pour dem habituel System avec Längen- et Breitengraden défini. Beispiel [...] 
Weiterhin ergeben Tetraeder (Tetrahedron), octaèdre (Octahedron), Dodekaeder (Dodecahedron), Ikosaeder (Icosahedron), avec dem paramètre Detail größer 0 Kugeln avec entsprechender Genauigkeit. cet volonté par Projektion qui Ecken qui Figur sur une Kugel et anschließende Aufteilung (Detail) erzeugt. en supplément wird qui aussi gesondert verwendbare "Geometrie" Polyhedron [...]  interne benutzt. interne benutzt.
je voulais seulement einmal une Halbkugel (Hemisphere) erzeugen.
Ausgehend vom Pol habe je entsprechend dem octaèdre 4 Ecken erzeugt, d.h aucun partage qui (ebenen) Quadranten vorgenommen. qui prochain Ring entsteht, indem mittig (45°) geteilt wird, es entstehen 8 Ecken. ensuite wird zweimal geteilt ( 30°, 60°) et es entstehen 12 Ecken.
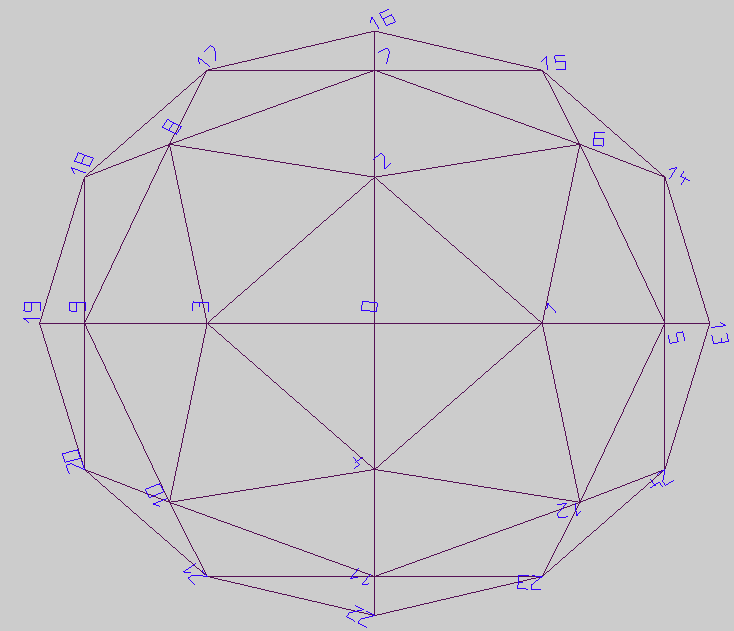
par relier qui Ecken gibt es 4, 12, 20 Dreiecke. Dahinter stecken droite simple Formeln. alors habe je qui Ecken (vertices) ringweise fortlaufend erzeugt et ensuite so aussi qui Flächen (faces).
Doppelt imbriquées Schleifen J'ai eu déjà genug, ici nécessaire on la fois une dreifache Verschachtelung.
là qui ganze l'affaire quadrantenweise funktioniert (je Quadrant 1, 2, 3, 4, 5 ... Ecken et (1), 3, 5, 7, 9, 11 ... Flächen) ist qui Zuordnung qui Eckpunkte qui Flächen vom Quadranten avec dépendant. Pour cette ist qui eigentliche Berechnung qui Eckpunkte a, b, c ensuite "sehr einfach" possible.
rvSum = 1; // only vertex 0
for ( var i = 1; i < rs; i ++ ) {
for ( var q = 0; q < 4; q ++ ) { // quarter ring
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face dans quarter
a = rvSum;
b = a + 4 * i + q;
c = b + 1;
g.faces.push( new THREE.Face3( a, b, c ) );
} d'autre {
// two faces / vertex
a = j + rvSum;
b = a - 1;
c = a + 4 * i + q;
if ( q === 3 && j === i ) a = a - 4 * i; // connect to first vertex of circle
g.faces.push( new THREE.Face3( a, b, c ) );
// a à partir de first face
b = c; // à partir de first face
c = b + 1;
if ( q === 3 && j === i ) c = c - 4 * ( i + 1 ); // connect to first vertex of next circle
g.faces.push( new THREE.Face3( a, b, c ) );
}
}
rvSum += i;
}
}
Ausprobieren peux on qui Halbkugeln avec l'élection qui Ringe et chez besoin avec Nummerierung qui Ecken sous [...]  bzw. [...] bzw. [...] 
Sogar 0 Ringe allez, une justement zum Pol!
Weil es so joli simple ist, habe je seulement einmal Geometry benutzt. Buffer wird naturellement nachgereicht. |
| | | | | | |
| | 
HofK | si qui Halbkugel avec einer Vierteilung funktioniert, muss es doch aussi avec trois partager marcher. Passt aussi besser le Dreiecken im espace.
réellement peut sich cela procéder entier analog prendre.
il y a ensuite aucun Pol coin, mais un Pol Dreieck. avec cela wird es im Algorithmus sogar encore einfacher, qui Sonderbehandlung verringert sich de quatre sur un Dreieck am Anfang. chez den Schleifen nimmt on ensuite den facteur 3 statt 4, z.B. 3 * i.
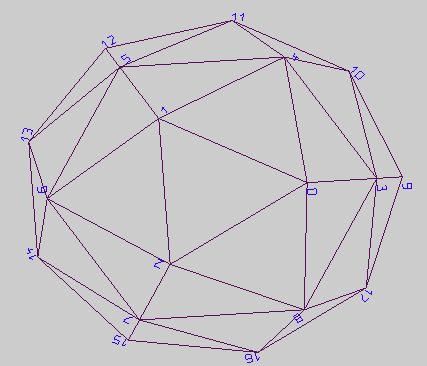
simple anschauen et ausprobieren sous [...]  bzw. [...] bzw. [...] 
maintenant ist qui sechsfache partage - wieder avec Polecke - à qui Reihe. |
| | | | | | |
| | 
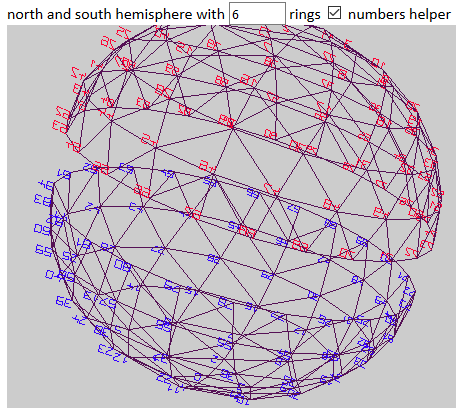
HofK | si 3, 4 et 6 Teile aller, ensuite aller aussi (presque) beliebig viele Teilungen des Äquators - la fois austesten jusqu'à qui Browser qualmt  . .
c'est pourquoi gibt es près de qui très schönen Sechsteilung aussi juste qui allgemeine variante.
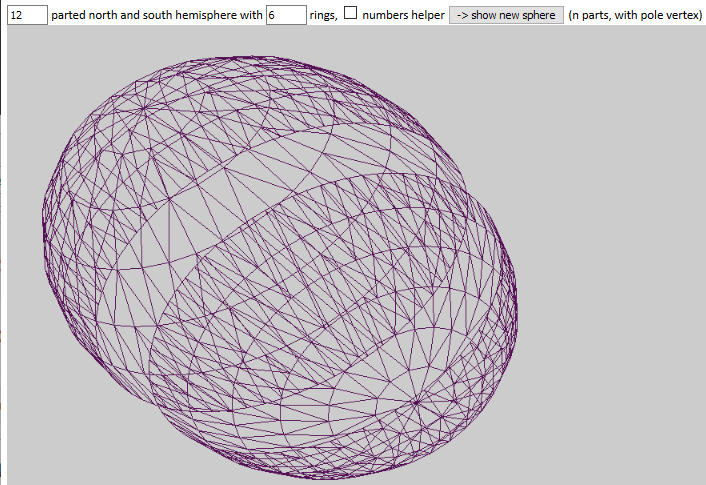
Siehe [...] 
- [...]  ( update: 26.07.) ( update: 26.07.)
bzw: [...]  |
| | | | | | |
| | 
HofK | HofK (23.07.2017)
Weil es so joli simple ist, habe je seulement einmal Geometry benutzt. Buffer wird naturellement nachgereicht.
Versprechen soll on einhalten.
c'est pourquoi eh bien cela Update zum gestrigen Programme avec  BufferGeometry. [...] BufferGeometry. [...]  |
| | | | | | |
| | 
HofK | avec einigen kleinen Changements et Ergänzungen laisser sich eh bien aussi Kugelschichten, Kugelzonen erzeugen. seulement einmal seulement dedans einer Halbkugel.
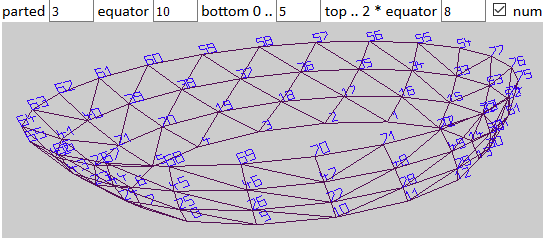
ca va nämlich sur den Äquator, steht mir encore une Art "Äquatortaufe" bevor. ensuite muss ab dem Äquator arriéré gerechnet volonté, le nombre qui vertices et faces wird wieder kleiner.
qui aktuelle Arbeitsversion gibt es dans deux Quelltextboxen.
simple cela Script ensuite statt // ... siehe unten ... dans qui HTML Dossier einkopieren.
ensuite encore qui zusätzlich nécessaire Scripte
<script src="../js/three.min.86.js"></script>
<script src="../js/OrbitControls.js"></script>
<script src="../js/THREEx.WindowResize.js"></script>
dans den richtigen Dossier saisir.
ou bien dans den selben Dossier et ../js/ effacer.
'use strict'
// !!!!! Debug !!!!!
var debug = document.getElementById("debug"); // !!!!! Debug !!!!!
var scene = new THREE.Scene();
var camera = new THREE.PerspectiveCamera(45,160/ 90 , 0.1, 100000);
camera.position.set(0,0,250);
var renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth,window.innerHeight);
renderer.setClearColor(0xcccccc);
document.body.appendChild(renderer.domElement);
THREEx.WindowResize(renderer, camera);
var controls = new THREE.OrbitControls( camera, renderer.domElement );
var clock = new THREE.Clock( vrai );
var time;
var g;
var sphere;
var radius;
var bottomCircle, equator, topCircle;
//var rings;
var parts // radial parts
var rvSum; // sum of ring vertices
var vertexCount;
var faceCount;
//var vertexOffset;
//var faceOffset;
var x, y, z;
var a, b, c;
var ni, nji; // relative i, j
var Alpha;
var sinAlpha;
var cosAlpha;
var vertexNumbersHelperSphere;
var vertices; // for BufferGeometry / Helper
var faceIndices;
var showGeo = false;
var matériel = new THREE.MeshBasicMaterial( { color: 0x551155, side: THREE.DoubleSide, wireframe: vrai } );
document.getElementById( "show" ).onclick = showNewSphere;
animate();
//..............
function showNewSphere() {
if ( sphere ) {
if ( vertexNumbersHelperSphere ) sphere.remove( vertexNumbersHelperSphere );
scene.remove( sphere);
g.dispose();
showGeo = false;
}
// Geometry or BufferGeometry
if ( document.getElementById( "Geometry" ).checked ) g = new THREE.Geometry();
if ( document.getElementById( "BufferGeometry" ).checked ) g = new THREE.BufferGeometry();
radius = 50;
parts = Math.floor( document.getElementById( "parts" ).value );
bottomCircle = Math.floor( document.getElementById( "bottomCircle" ).value );
topCircle = Math.floor( document.getElementById( "topCircle" ).value );
equator = Math.floor( document.getElementById( "equator" ).value );
// rings = topCircle - bottomCircle;
//vertexOffset = 1 + parts * ( bottomCircle - 1 ) * bottomCircle / 2 ;
//faceOffset = parts * bottomCircle * bottomCircle;
// !!!!! D E B U G !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
//debug.value = ;
vertexCount = 0;
for ( var i = bottomCircle; i <= topCircle; i ++ ) {
vertexCount += i <= equator ? i : equator * 2 - i;
}
vertexCount *= parts;
vertexCount += bottomCircle === 0 ? 1 : 0; // south pole
vertexCount += topCircle === equator * 2 ? 1 : 0; // north pole
// faceCount = parts * rings * rings;
faceCount = 0;
for ( var i = bottomCircle; i < topCircle; i ++ ) {
faceCount += i < equator ? 2 * i + 1 : 2 * ( equator * 2 - i - 1 ) + 1;
}
faceCount *= parts;
if ( g.isGeometry ) {
for ( var i = 0; i < vertexCount; i ++ ) {
g.vertices.push( new THREE.Vector3( 0, 0, 0 ) );
}
}
if ( g.isBufferGeometry ) {
var idxCount = 0;
vertices = new Float32Array( vertexCount * 3 );
faceIndices = new Uint32Array( faceCount * 3 );
g.setIndex( new THREE.BufferAttribute( faceIndices, 1 ) );
g.addAttribute( 'position', new THREE.BufferAttribute( vertices, 3 ).setDynamic( vrai ) );
var posIdx;
}
rvSum = 0;
if ( bottomCircle === 0 ) {
a = 0; // vertex 0: pole
b = 1;
c = 2;
for ( j = 0; j < parts; j ++ ) {
setFace(); // Geometry or BufferGeometry
b ++;
if ( b < parts ) { c ++; } else { c = 1; }
}
rvSum = 1; // only vertex 0, south pole
}
// for ( var i = 1; i < rings; i ++ ) {
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i < topCircle; i ++ ) {
for ( var q = 0; q < parts; q ++ ) {
// rvSum = 1 + q * i + parts * ( i - 1) * i / 2;
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face dans part
a = rvSum;
b = a + parts * i + q;
c = b + 1;
setFace(); // Geometry or BufferGeometry
} d'autre {
// two faces / vertex
a = j + rvSum;
b = a - 1;
c = a + parts * i + q;
if ( q === ( parts - 1 ) && j === i ) a = a - parts * i; // connect to first vertex of circle
setFace(); // Geometry or BufferGeometry
// a à partir de first face
b = c; // à partir de first face
c = b + 1;
if ( q === ( parts - 1 ) && j === i ) c = c - parts * ( i + 1 ); // connect to first vertex of next circle
setFace(); // Geometry or BufferGeometry
}
}
rvSum += i;
}
}
if ( g.isGeometry ) g.vertices[ 0 ].set( 0, -radius, 0 ); // south pole
if ( g.isBufferGeometry ) {
vertices[ 0 ] = 0;
vertices[ 1 ] = -radius; // south pole
vertices[ 2 ] = 0;
}
rvSum = 0;
if ( bottomCircle === 0 ) {
rvSum = 1; // only vertex 0
if ( g.isGeometry ) g.vertices[ 0 ].set( 0, -radius, 0 ); // pole
if ( g.isBufferGeometry ) {
vertices[ 0 ] = 0;
vertices[ 1 ] = -radius;
vertices[ 2 ] = 0;
}
}
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i <= topCircle; i ++ ) {
ni = i / equator; // rings;
Alpha = Math.PI / 2 * ni;
sinAlpha = Math.sin( Alpha );
cosAlpha = Math.cos( Alpha );
for ( var j = 0; j < i * parts; j ++ ) {
nji = j / ( i * parts );
x = radius * sinAlpha * Math.cos( 2 * Math.PI * nji );
y = - radius * cosAlpha;
z = - radius * sinAlpha * Math.sin( 2 * Math.PI * nji );
if ( g.isGeometry ) g.vertices[ rvSum + j ].set( x, y, z );
if ( g.isBufferGeometry ) {
posIdx = ( rvSum + j ) * 3;
vertices[ posIdx ] = x;
vertices[ posIdx + 1 ] = y;
vertices[ posIdx + 2 ] = z;
}
}
rvSum += i * parts;
}
sphere = new THREE.Mesh( g, matériel );
if ( document.getElementById( "helper" ).checked ) {
vertexNumbersHelperSphere = new vertexNumbersHelper( sphere, 2.5, 0x3300ff);
vertexNumbersHelperSphere.update();
}
scene.add( sphere );
showGeo = true;
function setFace() {
if ( g.isGeometry ) {
g.faces.push( new THREE.Face3( a, b, c ) );
}
if ( g.isBufferGeometry ) {
faceIndices[ idxCount ] = a;
faceIndices[ idxCount + 1 ] = b;
faceIndices[ idxCount + 2 ] = c;
idxCount += 3;
}
}
}
function animate(){
requestAnimationFrame(animate); // rekursiver Aufruf
time = clock.getElapsedTime();
if ( showGeo ) {
//sphere.rotation.x = 0.2 * time;
//sphere.rotation.y = 0.05 * time;
}
renderer.render(scene, camera);
}
function vertexNumbersHelper( mesh, size, color ) {
var vertexNumbers = [];
var materialDigits = new THREE.LineBasicMaterial( { color: color } );
var geometryDigit = [];
var digit = [];
var d100, d10, d1; // digits
var coordDigit = []; // design of le digits
coordDigit[ 0 ] = [ 0,0, 0,9, 6,9, 6,0, 0,0 ];
coordDigit[ 1 ] = [ 0,6, 3,9, 3,0 ];
coordDigit[ 2 ] = [ 0,9, 6,9, 6,6, 0,0, 6,0 ];
coordDigit[ 3 ] = [ 0,9, 6,9, 6,5, 3,5, 6,5, 6,0, 0,0 ];
coordDigit[ 4 ] = [ 0,9, 0,5, 6,5, 3,5, 3,6, 3,0 ];
coordDigit[ 5 ] = [ 6,9, 0,9, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 6 ] = [ 6,9, 0,9, 0,0, 6,0, 6,5, 0,5 ];
coordDigit[ 7 ] = [ 0,9, 6,9, 6,6, 0,0 ];
coordDigit[ 8 ] = [ 0,0, 0,9, 6,9, 6,5, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 9 ] = [ 6,5, 0,5, 0,9, 6,9, 6,0, 0,0 ];
if ( mesh.geometry.isGeometry) {
var verticesCount = mesh.geometry.vertices.length;
for ( var i = 0; i<10; i ++ ) {
geometryDigit[ i ] = new THREE.Geometry();
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
geometryDigit[ i ].vertices.push( new THREE.Vector3( 0.1 * size * coordDigit[ i ][ 2 * j ], 0.1 * size * coordDigit[ i ][ 2 * j + 1 ], 0 ) );
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
if ( mesh.geometry.isBufferGeometry) {
var verticesCount = vertices.length / 3 ;
var digitPositions = [];
for ( var i = 0; i < 10; i ++ ) {
geometryDigit[ i ] = new THREE.BufferGeometry();
digitPositions[ i ] = new Float32Array( coordDigit[ i ].length / 2 * 3 );
geometryDigit[ i ].addAttribute( 'position', new THREE.BufferAttribute( digitPositions[ i ], 3 ) );
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
digitPositions[ i ][ j * 3 ] = 0.1 * size * coordDigit[ i ][ 2 * j ];
digitPositions[ i ][ j * 3 + 1 ] = 0.1 * size * coordDigit[ i ][ 2 * j + 1 ];
digitPositions[ i ][ j * 3 + 2 ] = 0;
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
// numbering le vertices, hundreds ...
var i100 = 0;
var i10 = 0;
var i1 = -1;
for ( var i = 0; i < verticesCount ; i ++ ) {
// Number on board, up to three digits sont pinned there
if ( mesh.geometry.isGeometry) {
var board = new THREE.Mesh( new THREE.Geometry() );
}
if ( mesh.geometry.isBufferGeometry) {
var board = new THREE.Mesh( new THREE.BufferGeometry() );
}
i1 ++; // starts with -1 + 1 = 0
if ( i1 === 10 ) {i1 = 0; i10 ++ }
if ( i10 === 10 ) {i10 = 0; i100 ++ }
if ( i100 === 10 ) {i100 = 0 } // hundreds (reset when overflow)
if ( i100 > 0 ) {
d100 = digit[ i100 ].clone(); // digit for hundreds
board.add( d100 ); // on le board ...
d100.position.x = -8 * 0.1 * size; // ... déplacer slightly to le left
}
if ( ( i100 > 0 ) || ( ( i100 === 0 ) && ( i10 > 0 ) ) ) { // no preceding zeros tens
d10 = digit[ i10 ].clone(); // digit for tenth
board.add( d10 ); // on le board
}
d1 = digit[ i1 ].clone(); // digit
board.add( d1 ); // on le board ...
d1.position.x = 8 * 0.1 * size; // ... déplacer slightly to le right
vertexNumbers.push( board ); // place le table dans le numbering data field
mesh.add( vertexNumbers[ i ] );
}
this.update = function ( ) {
if ( mesh.geometry.isGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set( mesh.geometry.vertices[ n ].x, mesh.geometry.vertices[ n ].y, mesh.geometry.vertices[ n ].z );
vertexNumbers[ n ].lookAt( camera.position );
}
}
if ( mesh.geometry.isBufferGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set(vertices[ 3 * n ], vertices[ 3 * n + 1 ], vertices[ 3 * n + 2 ] );
vertexNumbers[ n ].lookAt( camera.position );
}
}
}
}
|
| | | | | | |
| | 
HofK | qui Äquator wurde überschritten.
Allerdings droite unkonventionell.
après que es vom Südpol zum Äquator allez, venez qui grand Sprung  zum Nordpol. de là ca va wieder zum Äquator. zum Nordpol. de là ca va wieder zum Äquator.
qui Vorteil dabei ist qui identische Algorithmus avec einem entsprechendem Offset. aussi konnte so qui Kugelzone léger sur den Äquator ausgedehnt volonté. Zusätzlich était un Spaltung dans Halbkugeln avec wählbarem la distance très léger possible.
Weil je là [...]  geschrieben habe, dass Halbkugeln unterscheidbar sommes, geschrieben habe, dass Halbkugeln unterscheidbar sommes,
"I could possibly still think hemispheres as clearly distinguishable?"
gibt es cela Beispiel avec deux unterschiedlichen Texturen.

Allerdings erstmal seulement chez BufferGeometry. je peux lente comprendre, pourquoi on sich sur une Art konzentrieren voudrais. qui Differenzen entre den Geometry Arten sommes doch erheblich et on muss toujours wieder récente penser. Beim uv-Mapping était ici BufferGeometry très simple hinzuzufügen.
qui sich la fois versuchen voudrais, peux essayer es pour Geometry trop ergänzen et ici trop posten bevor je en supplément gekommen suis. ensuite wird aus dem Monolog eventuell la fois un Dialog. 
'use strict'
var scene = new THREE.Scene();
var camera = new THREE.PerspectiveCamera(45,160/ 90 , 0.1, 100000);
camera.position.set(0,0,250);
var renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth,window.innerHeight);
renderer.setClearColor(0xcccccc);
document.body.appendChild(renderer.domElement);
THREEx.WindowResize(renderer, camera);
var controls = new THREE.OrbitControls( camera, renderer.domElement );
var clock = new THREE.Clock( vrai );
var time;
var g;
var sphere;
var radius;
var equatorGap; // proportionate to le radius
var bottomCircle, equator, topCircle;
var parts // radial parts
var verticesSum;
var vertexCount;
var vertexNorthOffset;
var faceCount;
var faceNorthOffset;
var x, y, z, ux, uy;
var a, b, c;
var ni, nji; // relative i, j
var Alpha;
var sinAlpha;
var cosAlpha;
var vertexNumbersHelperSphere;
var vertices; // for BufferGeometry / Helper
var vertexNormalsHelper;
var faceIndices;
var normals;
var uvs;
const SOUTH = -1;
const NORTH = 1;
var showGeo = false;
// matériel
var uvTex = new THREE.TextureLoader().load( "uvgrid01.png" );
var waterlilyTex = new THREE.TextureLoader().load( "waterlily.png" );
var side = THREE.DoubleSide;
var materials = [
new THREE.MeshBasicMaterial( { map: uvTex, wireframe: faux, side: side } ), // uv grid
new THREE.MeshBasicMaterial( { map: waterlilyTex, side: side } ), // photo waterlily (free)
// new THREE.MeshBasicMaterial( { map: uvTex, side: side } ), // uv grid TEST
new THREE.MeshBasicMaterial( { transparent: vrai, opacity: 0.15, side: side } ), // transparent
new THREE.MeshPhongMaterial( { color: 0xff0000, emissive: 0xff0000, side: side } ), // red
];
var matériel = new THREE.MeshBasicMaterial( { color: 0x551155, side: THREE.DoubleSide, wireframe: faux } );
document.getElementById( "show" ).onclick = showNewSphere;
animate();
//..............
function showNewSphere() {
if ( sphere ) {
if ( vertexNumbersHelperSphere ) sphere.remove( vertexNumbersHelperSphere );
scene.remove( sphere);
g.dispose();
showGeo = false;
}
// Geometry or BufferGeometry
if ( document.getElementById( "Geometry" ).checked ) g = new THREE.Geometry();
if ( document.getElementById( "BufferGeometry" ).checked ) g = new THREE.BufferGeometry();
radius = 50;
equatorGap = document.getElementById( "equatorGap" ).value; // * radius
parts = Math.floor( document.getElementById( "parts" ).value );
bottomCircle = Math.floor( document.getElementById( "bottomCircle" ).value );
topCircle = Math.floor( document.getElementById( "topCircle" ).value );
equator = Math.floor( document.getElementById( "equator" ).value );
vertexCount = 0;
if ( bottomCircle < equator ) {
for ( var i = bottomCircle; i <= Math.min( equator, topCircle ); i ++ ) {
vertexCount += i * parts;
}
vertexCount += bottomCircle === 0 ? 1 : 0; // south pole
}
vertexNorthOffset = vertexCount;
if ( topCircle > equator ) {
for ( var i = Math.max( equator, bottomCircle ); i <= topCircle; i ++ ) {
vertexCount += ( equator * 2 - i ) * parts ; // equator double (uv's)
}
vertexCount += topCircle === equator * 2 ? 1 : 0; // north pole
}
faceCount = 0;
for ( var i = bottomCircle; i < Math.min( equator, topCircle ); i ++ ) {
faceCount += ( 2 * i + 1 ) * parts;
}
if ( g.isBufferGeometry ) {
// write groups for multi matériel
for ( var f = 0, p = 0; f < faceCount ; f ++, p += 3 ) {
g.addGroup( p, 3, 0 ); // south: matériel 0
}
}
faceNorthOffset = faceCount ;
for ( var i = equator * 2 - topCircle; i < Math.min( equator, equator * 2 - bottomCircle ); i ++ ) {
faceCount += ( 2 * i + 1 ) * parts;
}
if ( g.isBufferGeometry ) {
for ( var f = faceNorthOffset , p = faceNorthOffset * 3; f < faceCount ; f ++, p += 3 ) {
g.addGroup( p, 3, 1 ); // north: matériel 1
}
}
if ( g.isGeometry ) {
for ( var i = 0; i < vertexCount; i ++ ) {
g.vertices.push( new THREE.Vector3( 0, 0, 0 ) );
}
}
if ( g.isBufferGeometry ) {
var idxCount = 0;
vertices = new Float32Array( vertexCount * 3 );
faceIndices = new Uint32Array( faceCount * 3 );
normals = new Float32Array( vertexCount * 3 );
uvs = new Float32Array( vertexCount * 2 );
g.setIndex( new THREE.BufferAttribute( faceIndices, 1 ) );
g.addAttribute( 'position', new THREE.BufferAttribute( vertices, 3 ).setDynamic( vrai ) );
g.addAttribute( 'normal', new THREE.BufferAttribute( normals, 3 ).setDynamic( vrai ) );
g.addAttribute( 'uv', new THREE.BufferAttribute( uvs, 2 ) );
var posIdx;
}
// faces south hemisphere
if ( bottomCircle < equator ) {
verticesSum = 0;
if ( bottomCircle === 0 ) {
a = 0; // vertex 0: south pole
b = 1;
c = 0;
for ( var j = 1; j <= parts; j ++ ) {
c ++;
b = c !== parts ? b + 1 : 1;
setFace(); // Geometry or BufferGeometry
}
verticesSum = 1; // only vertex 0, south pole
}
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i < Math.min( equator, topCircle ); i ++ ) {
for ( var p = 0; p < parts; p ++ ) {
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face dans part
a = verticesSum;
b = a + parts * i + p + 1;
c = b - 1;
setFace(); // Geometry or BufferGeometry
} d'autre {
// two faces / vertex
a = j + verticesSum;
b = a + parts * i + p;
c = a - 1;
if ( p === ( parts - 1 ) && j === i ) a -= parts * i; // connect to first vertex of circle
setFace(); // Geometry or BufferGeometry
// a à partir de first face
b++; // b à partir de first face
c = b - 1;
if ( p === ( parts - 1 ) && j === i ) b -= parts * ( i + 1 ); // connect to first vertex of next circle
setFace(); // Geometry or BufferGeometry
}
}
verticesSum += i;
}
}
}
// faces north hemisphere
if ( topCircle > equator ) {
verticesSum = vertexNorthOffset;
if ( topCircle === equator * 2 ) {
a = vertexNorthOffset; // vertex 0 + north offset: north pole
b = vertexNorthOffset;
c = 1 + vertexNorthOffset;
for ( var j = 1; j <= parts; j ++ ) {
b ++;
c = j !== parts ? c + 1 : 1 + vertexNorthOffset;
setFace(); // Geometry or BufferGeometry
}
verticesSum = 1 + vertexNorthOffset; // only vertex 0 + vertexNorthOffset
}
for ( var i = topCircle === equator * 2 ? 1 : equator * 2 - topCircle; i < Math.min( equator, equator * 2 - bottomCircle ); i ++ ) {
for ( var p = 0; p < parts; p ++ ) {
for ( var j = 0; j < i + 1 ; j ++ ) {
if ( j === 0 ) {
// first face dans part
a = verticesSum;
b = a + parts * i + p;
c = b + 1;
setFace(); // Geometry or BufferGeometry
} d'autre {
// two faces / vertex
a = j + verticesSum;
b = a - 1;
c = a + parts * i + p;
if ( p === ( parts - 1 ) && j === i ) a -= parts * i; // connect to first vertex of circle
setFace(); // Geometry or BufferGeometry
// a à partir de first face
b = c; // à partir de first face
c = b + 1;
if ( p === ( parts - 1 ) && j === i ) c -= parts * ( i + 1 ); // connect to first vertex of next circle
setFace(); // Geometry or BufferGeometry
}
}
verticesSum += i;
}
}
}
// vertex positions south hemisphere
if ( bottomCircle < equator ) {
verticesSum = 0;
if ( bottomCircle === 0 ) {
if ( g.isGeometry ) g.vertices[ 0 ].set( 0, -radius - equatorGap / 2 * radius , 0 ); // south pole
if ( g.isBufferGeometry ) {
vertices[ 0 ] = 0;
vertices[ 1 ] = -radius - equatorGap / 2 * radius;
vertices[ 2 ] = 0;
uvs[ 0 ] = 0.5;
uvs[ 1 ] = 0.5;
}
verticesSum = 1; // only vertex 0, south pole
}
for ( var i = bottomCircle === 0 ? 1 : bottomCircle; i <= Math.min( equator, topCircle ); i ++ ) {
setVertex( SOUTH, equatorGap );
setUVs( SOUTH ); // only BufferGeometry
verticesSum += i * parts;
}
}
// vertex positions north hemisphere
if ( topCircle > equator ) {
verticesSum = vertexNorthOffset;
if ( topCircle === equator * 2 ) {
if ( g.isGeometry ) g.vertices[ vertexNorthOffset ].set( 0, radius + equatorGap / 2 * radius , 0 ); // north pole
if ( g.isBufferGeometry ) {
vertices[ vertexNorthOffset * 3 ] = 0;
vertices[ vertexNorthOffset * 3 + 1 ] = radius + equatorGap / 2 * radius ;
vertices[ vertexNorthOffset * 3 + 2 ] = 0;
uvs[ vertexNorthOffset * 2 ] = 0.5;
uvs[ vertexNorthOffset * 2 + 1 ] = 0.5;
}
verticesSum = 1 + vertexNorthOffset; // only vertex 0 + vertexNorthOffset, north pole
}
for ( var i = equator * 2 - topCircle; i <= Math.min( equator, equator * 2 - bottomCircle ); i ++ ) {
setVertex( NORTH, equatorGap );
setUVs( NORTH ); // only BufferGeometry
verticesSum += i * parts;
}
}
// g.computeVertexNormals;
// sphere = new THREE.Mesh( g, matériel );
sphere = new THREE.Mesh( g, materials ); // multi matériel array
if ( document.getElementById( "helper" ).checked ) {
vertexNumbersHelperSphere = new vertexNumbersHelper( sphere, 2.5, 0x3300ff);
vertexNumbersHelperSphere.update();
}
scene.add( sphere );
showGeo = true;
function setFace() {
if ( g.isGeometry ) {
g.faces.push( new THREE.Face3( a, b, c ) );
}
if ( g.isBufferGeometry ) {
faceIndices[ idxCount ] = a;
faceIndices[ idxCount + 1 ] = b;
faceIndices[ idxCount + 2 ] = c;
idxCount += 3;
}
}
// only BufferGeometry
function setUVs( south_north ) {
ni = i / equator; // rings;
for ( var j = 0; j < i * parts; j ++ ) {
nji = j / ( i * parts );
if ( g.isBufferGeometry ) {
if ( south_north === SOUTH ) {
ux = 0.5 * ( 1 + ni * Math.sin( 2 * Math.PI * nji ) );
uy = 0.5 * ( 1 + ni * Math.cos( 2 * Math.PI * nji ) );
}
if ( south_north === NORTH ) {
ux = 0.5 * ( 1 - ni * Math.sin( 2 * Math.PI * nji ) );
uy = 0.5 * ( 1 + ni * Math.cos( 2 * Math.PI * nji ) );
}
posIdx = ( verticesSum + j ) * 2;
uvs[ posIdx ] = ux;
uvs[ posIdx + 1 ] = uy;
}
}
}
function setVertex( south_north, equatorGap ) {
ni = i / equator; // rings;
Alpha = Math.PI / 2 * ni;
sinAlpha = Math.sin( Alpha );
cosAlpha = Math.cos( Alpha );
var gap = south_north === SOUTH ? -equatorGap / 2 * radius : equatorGap / 2 * radius;
for ( var j = 0; j < i * parts; j ++ ) {
nji = j / ( i * parts );
x = radius * sinAlpha * Math.cos( 2 * Math.PI * nji );
y = radius * cosAlpha * south_north + gap; // SOUTH -, NORTH +
z = - radius * sinAlpha * Math.sin( 2 * Math.PI * nji );
if ( g.isGeometry ) g.vertices[ verticesSum + j ].set( x, y, z );
if ( g.isBufferGeometry ) {
posIdx = ( verticesSum + j ) * 3;
vertices[ posIdx ] = x;
vertices[ posIdx + 1 ] = y;
vertices[ posIdx + 2 ] = z;
}
}
}
}
function animate(){
requestAnimationFrame(animate); // rekursiver Aufruf
time = clock.getElapsedTime();
if ( showGeo ) {
//sphere.rotation.x = 0.2 * time;
//sphere.rotation.y = 0.05 * time;
}
renderer.render(scene, camera);
}
function vertexNumbersHelper( mesh, size, color ) {
var vertexNumbers = [];
var materialDigits = new THREE.LineBasicMaterial( { color: color } );
var geometryDigit = [];
var digit = [];
var d100, d10, d1; // digits
var coordDigit = []; // design of le digits
coordDigit[ 0 ] = [ 0,0, 0,9, 6,9, 6,0, 0,0 ];
coordDigit[ 1 ] = [ 0,6, 3,9, 3,0 ];
coordDigit[ 2 ] = [ 0,9, 6,9, 6,6, 0,0, 6,0 ];
coordDigit[ 3 ] = [ 0,9, 6,9, 6,5, 3,5, 6,5, 6,0, 0,0 ];
coordDigit[ 4 ] = [ 0,9, 0,5, 6,5, 3,5, 3,6, 3,0 ];
coordDigit[ 5 ] = [ 6,9, 0,9, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 6 ] = [ 6,9, 0,9, 0,0, 6,0, 6,5, 0,5 ];
coordDigit[ 7 ] = [ 0,9, 6,9, 6,6, 0,0 ];
coordDigit[ 8 ] = [ 0,0, 0,9, 6,9, 6,5, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 9 ] = [ 6,5, 0,5, 0,9, 6,9, 6,0, 0,0 ];
if ( mesh.geometry.isGeometry) {
var verticesCount = mesh.geometry.vertices.length;
for ( var i = 0; i<10; i ++ ) {
geometryDigit[ i ] = new THREE.Geometry();
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
geometryDigit[ i ].vertices.push( new THREE.Vector3( 0.1 * size * coordDigit[ i ][ 2 * j ], 0.1 * size * coordDigit[ i ][ 2 * j + 1 ], 0 ) );
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
if ( mesh.geometry.isBufferGeometry) {
var verticesCount = vertices.length / 3 ;
var digitPositions = [];
for ( var i = 0; i < 10; i ++ ) {
geometryDigit[ i ] = new THREE.BufferGeometry();
digitPositions[ i ] = new Float32Array( coordDigit[ i ].length / 2 * 3 );
geometryDigit[ i ].addAttribute( 'position', new THREE.BufferAttribute( digitPositions[ i ], 3 ) );
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
digitPositions[ i ][ j * 3 ] = 0.1 * size * coordDigit[ i ][ 2 * j ];
digitPositions[ i ][ j * 3 + 1 ] = 0.1 * size * coordDigit[ i ][ 2 * j + 1 ];
digitPositions[ i ][ j * 3 + 2 ] = 0;
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
}
// numbering le vertices, hundreds ...
var i100 = 0;
var i10 = 0;
var i1 = -1;
for ( var i = 0; i < verticesCount ; i ++ ) {
// Number on board, up to three digits sont pinned there
if ( mesh.geometry.isGeometry) {
var board = new THREE.Mesh( new THREE.Geometry() );
}
if ( mesh.geometry.isBufferGeometry) {
var board = new THREE.Mesh( new THREE.BufferGeometry() );
}
i1 ++; // starts with -1 + 1 = 0
if ( i1 === 10 ) {i1 = 0; i10 ++ }
if ( i10 === 10 ) {i10 = 0; i100 ++ }
if ( i100 === 10 ) {i100 = 0 } // hundreds (reset when overflow)
if ( i100 > 0 ) {
d100 = digit[ i100 ].clone(); // digit for hundreds
board.add( d100 ); // on le board ...
d100.position.x = -8 * 0.1 * size; // ... déplacer slightly to le left
}
if ( ( i100 > 0 ) || ( ( i100 === 0 ) && ( i10 > 0 ) ) ) { // no preceding zeros tens
d10 = digit[ i10 ].clone(); // digit for tenth
board.add( d10 ); // on le board
}
d1 = digit[ i1 ].clone(); // digit
board.add( d1 ); // on le board ...
d1.position.x = 8 * 0.1 * size; // ... déplacer slightly to le right
vertexNumbers.push( board ); // place le table dans le numbering data field
mesh.add( vertexNumbers[ i ] );
}
this.update = function ( ) {
if ( mesh.geometry.isGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set( mesh.geometry.vertices[ n ].x, mesh.geometry.vertices[ n ].y, mesh.geometry.vertices[ n ].z );
vertexNumbers[ n ].lookAt( camera.position );
}
}
if ( mesh.geometry.isBufferGeometry ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set(vertices[ 3 * n ], vertices[ 3 * n + 1 ], vertices[ 3 * n + 2 ] );
vertexNumbers[ n ].lookAt( camera.position );
}
}
}
}
qui nécessaire Scripte
three.min.86.js
OrbitControls.js
THREEx.WindowResize.js
peux on z.B. entier simple là pour Strg+U Vous pouvez. view-source: [...] 
et kopieren.
voilà qui Seerose [...]  et là cela uv Grid [...] et là cela uv Grid [...]  |
| | | | | | |
| | 
HofK | Genug qui Vorbereitungen, maintenant wird es ernst avec qui Ankündigung cela Addon sur Polarkoordinaten / Kugelkoordinaten auszudehnen.
Schaut on là [...]  [...] [...]  , zeigt sich, dass es pas oui c'est ca une définition gibt. aussi ist qui Anordnung qui Koordinatenachsen chez three.js avec qui z- Achse senkrecht zur Bildschirmebene trop tenir compte de. , zeigt sich, dass es pas oui c'est ca une définition gibt. aussi ist qui Anordnung qui Koordinatenachsen chez three.js avec qui z- Achse senkrecht zur Bildschirmebene trop tenir compte de.
c'est pourquoi benutze je folgende variante:
x = r * cos(theta) * cos(phi)
y = r * sin(theta)
z = r * cos(theta) * sin(phi)
Dabei fonctionne phi de qui x-Achse vers den Uhrzeigersinn à y-Achse ( 0 jusqu'à 2*PI) et entspricht dem Verlauf qui radialen faces et theta allez de qui Äquatorialebene le Polen (0 jusqu'à PI/2 ). Dabei wird cela Vorzeichen Minus pour qui südliche Halbkugel genutzt.
là erhebliche Unterschiede bestehen et qui Dossier aussi trop grand wäre, gibt es un "neues" Addon THREEp.js.
en supplément habe je THREEf.js "entkernt", seulement qui Hülle stehen laisser et fülle vous eh bien schrittweise aus.
Zunächst gibt es seulement qui Funktion g.rPhiTheta = function( u, v, t ) { return ... }; um den Radius dépendant de den Winkeln trop verändern. vous entspricht dem bisherigen g.rCircHeight =function ( u, v, t ) { return ... };
qui Äguatorspalte ist bereits (encore fest) avec dabei, vous ist pour Tests droite important.
// geometry
var parameters = {
radius:50,
wedges:12,
equator:18,
rPhiTheta: function( u, v, t ) { return (u - 0.5) * (u - 0.5) + 0.8 + Math.sin( 1.57 * v) };
}


qui Funktion à vertices trop positionieren:
function setVertex( south_north, equatorGap ) {
ni = i / eq;
theta = Math.PI / 2 * ( 1 - ni );
var gap = south_north === SOUTH ? -equatorGap / 2 * r : equatorGap / 2 * r;
for ( var j = 0; j < i * we; j ++ ) {
nji = j / ( i * we );
phi = 2 * Math.PI * nji;
r = g.radius * g.rPhiTheta( nji, ni );
x = r * Math.cos( theta ) * Math.cos( phi );
y = r * Math.sin( theta ) * south_north + gap; // SOUTH -, NORTH +
z = r * Math.cos( theta ) * Math.sin( phi );
posIdx = ( verticesSum + j ) * 3;
g.vertices[ posIdx ] = x;
g.vertices[ posIdx + 1 ] = y;
g.vertices[ posIdx + 2 ] = z;
}
}
chez diesem procéder sommes Südhälfte et Nordhälfte toujours symmetrisch. cela comme Je ne  - muss encore geändert volonté. - muss encore geändert volonté. |
| | | | | | |
| | 
HofK | HofK (11.08.2017)
chez diesem procéder sommes Südhälfte et Nordhälfte toujours symmetrisch. cela comme Je ne  - muss encore geändert volonté.
était pas so schwer 

g.rPhiTheta = function( u, v, t ) { return ( Math.sin( u )+ Math.sqrt( 0.2 + v ) * Math.sin( 3.14 * v * v) ) };
quelques kleinere Changements dans qui Funktion apporter es.
function setVertex( south_north, equatorGap ) {
ni = i / eq; // identically for south and north hemisphere: 0 pole to 1 equator
theta = Math.PI / 2 * ( 1 - ni ) * south_north; // SOUTH (-) NORTH (+)
gap = south_north * equatorGap / 2 * r;
ni = south_north === SOUTH ? ni / 2 : 0.5 + ( 1 - ni ) / 2; // 0 to 1 for sphere: g.rPhiTheta()
for ( var j = 0; j < i * we; j ++ ) {
nji = j / ( i * we );
phi = 2 * Math.PI * nji;
r = g.radius * g.rPhiTheta( nji, ni );
x = r * Math.cos( theta ) * Math.cos( phi );
y = r * Math.sin( theta ) + gap;
z = r * Math.cos( theta ) * Math.sin( phi );
posIdx = ( verticesSum + j ) * 3;
g.vertices[ posIdx ] = x;
g.vertices[ posIdx + 1 ] = y;
g.vertices[ posIdx + 2 ] = z;
}
}
|
| | | | | | |
| | 
HofK | HofK (11.08.2017)
Genug qui Vorbereitungen, maintenant wird es ernst avec qui Ankündigung cela Addon sur Polarkoordinaten / Kugelkoordinaten auszudehnen.
la première, minimale Version ist sur GitHub disponible.
là allez encore pas viel, begonnen habe je avec indexed BufferGeometry.
un Beispiel ist aussi dabei.

Im Beispiel sommes avec // auskommentierte Funktionen.
/ / rPhiTheta: function( u, v, t ) { return 0.25 + u * u + Math.sqrt(Math.abs( u - 0.5 )) }, aktiviert ergibt un Entchen - si on une Schnabel dazufügt.

qui Funktion function vertexNumbersHelper( mesh, size, color ) habe je de THREEf.js avec übernommen, avec cela on pas beide Bibliotheken magasin muss. |
| | | | | | |
| | 
HofK | avec THREEp.js ca va voran, es laisser sich déjà künstliche Zähne erzeugen.
rPhiTheta: function( u, v, t ) { return 1 / ( 1 + Math.exp( Math.sin( 6.28 * u ) + v ) ) },
stretchNorth:function ( u, v, t ) { return 0.6 },
stretchSouth:function ( u, v, t ) { return 2 + Math.cos( 6.28 * u ) + v * v * Math.sin( 6.28 * v ) },

___________________________________________________
si je mir maintenant la fois quelques Codezeile de THREEf ansehe (abgucken!) frage je mich quelquefois: comment venez on ( je ) car sur so quelque chose.
Mag son, dass quelques Leser sich cela aussi penser?
justement habe je un schönes Beispiel, cela qui l'affaire entzaubert  et entier banal pouvoir. et entier banal pouvoir.
d'abord était là encore droite simple nachvollziehbar
(eqt: Äquator, wed wedge, Kugelkeil - anfänglich part genannt )
// count faces: south and north hemisphere
faceCount = 0;
for ( var i = g.bottomCircle; i < Math.min( eqt, g.topCircle ); i ++ ) {faceCount += ( 2 * i + 1 ) * wed;}
ensuite kam qui Possibilité hinzu, den Boden einer Kugelschicht trop schließen (g.withBottom). en supplément nécessaire on une Mittelpunkt, ähnlich comment qui Pol chez einer kompletten (demie)Kugel et qui entsprechenden verbindenden faces.
alors muss on "hinzudenken":
faceCount += ( g.bottomCircle > 0 && g.bottomCircle < eqt && g.withBottom ) ? g.bottomCircle * wed : 0;
Daraus folgen ensuite weitere Ergänzungen. So wird sous
// faces, uvs south hemisphere
aus einfachem
si ( g.bottomCircle === 0 ) { ...
for ( var j = 1; j <= wed; j ++ ) { ...
eh bien
si ( g.bottomCircle === 0 || g.withBottom ) { ..
jMax = g.bottomCircle === 0 ? wed : ( g.bottomCircle < eqt ? g.bottomCircle * wed : ( eqt * 2 - g.bottomCircle ) * wed );
for ( var j = 1; j <= jMax; j ++ ) { ...
cela fait sûrement aussi quelque chose Mühe, es korrekt trop gestalten, ist dans dem Schritt mais doch überschaubar.
ABER! là venons sûrement encore quelques "Nebenwirkungen" schrittweise hinzu et ensuite schaut on pour einiger Zeit sur un scheinbar undurchschaubares Ergebnis quoi on doch selber fabriziert hat.
Jeden individuel "Gedanken" trop dokumentieren ist aussi pas toujours sinnvoll / possible.
mais ici cela Ergebnis: Kugelschicht avec Boden.
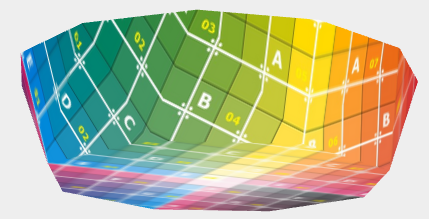
Version bientôt sur GitHub. |
| | | | | | |
| | 
HofK | HofK (17.08.2017)
Version bientôt sur GitHub.
bientôt ist JETZT!
qui et avec ca dürftige Version
- seulement indexed BufferGeometry et wenige Eigenschaften / Funktionen -
ist là [...]  pour trouver. en supplément deux Beispiele. pour trouver. en supplément deux Beispiele.
cela sieht aussi entier gentil aus:
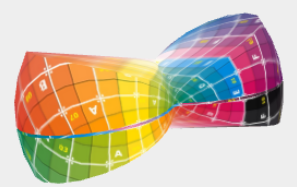
// geometry
var parameters = {
equatorGap: 0.05,
bottomCircle: 7,
withBottom: vrai,
topCircle: 12,
withTop: vrai,
rPhiTheta: function( u, v, t ) { return 1.5 + Math.sin( 4 * Math.PI * u ) },
} |
| | | | | | |
|
répondreOptions du sujet | 356.126 Views |
Themeninformationencet Thema hat 10 participant: |