PHP, HTML & JavaScript- Forum | | | | | | - Seite 1 - |
| 
HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
| | | | | | |
| | | | | | - Seite 13 - |
| | 
HofK |  da geht es weiter ... da geht es weiter ...
Eine Kugel ist überall schön rund, ein Oktaeder nur eckig und kantig.
Aber was liegt dazwischen?
Man kann ein Oktaeder stetig zu einer Kugel transformieren. Dazu benötigt man passende Zick Zack Funktionen.
Eine schöne Herleitung findet man da: [...] 
Mit dieser Hilfe ist die Transformation dann kein Problem. Im momentanen Testcode ist die Transformation noch als Konstante 0.5 eingetragen. Da muss noch ein Parameter mit Werten 0 bis 1 ersetzt werden.
In der xyz Berechnug wurde dann einfach sin durch sinlike und cos durch coslike ersetzt - fertig.
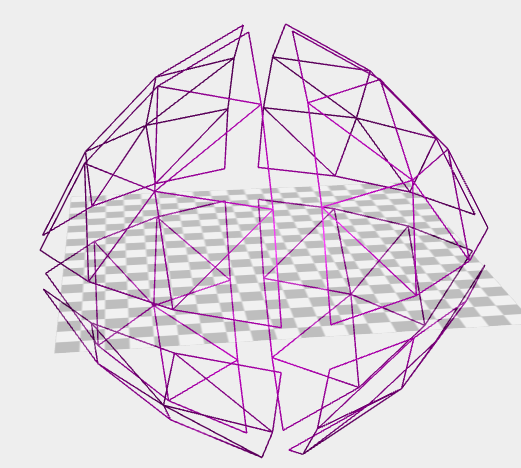
Die Konstruktion besteht aus 8 unabhängigen Teilen. Diese können mit einem Parameter drift auseinander geschoben werden - abhängig von der Zeit. Das habe ich im Bild gemacht. Dadurch ist auch die leichte Rundung gut zu erkennen.
Ohne Drift und mit passendem Parameter erhält man ein Oktaeder.
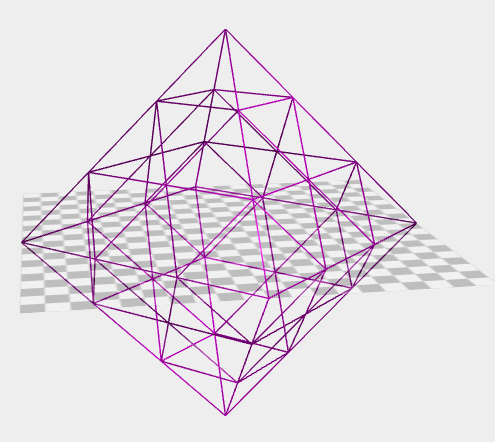 |
| | | | | | |
| | 
HofK | Auch andere 2Pi periodische Funktionen ergeben interessante Formen.
Um das schnell zu testen, habe ich mal XProfan benutzt. Damit geht das ohne großen Aufwand so nebenbei. Da ich in letzter Zeit fast nur mit JavaScript gearbeitet habe, ist es ebenfalls ganz gut, auch abweichende Syntax zu verwenden. Es wird ein Punkt mit x zwischen 0 und Pi/2 und y zwischen 0 und 1 - hier (0.5, 0.75) - angegeben. Daraus werden zwei Geradenabschnitte bestimmt. Nun wird durch entsprechende Zuordnung aus diesem Teilstück die periodische Funktion gebastelt.
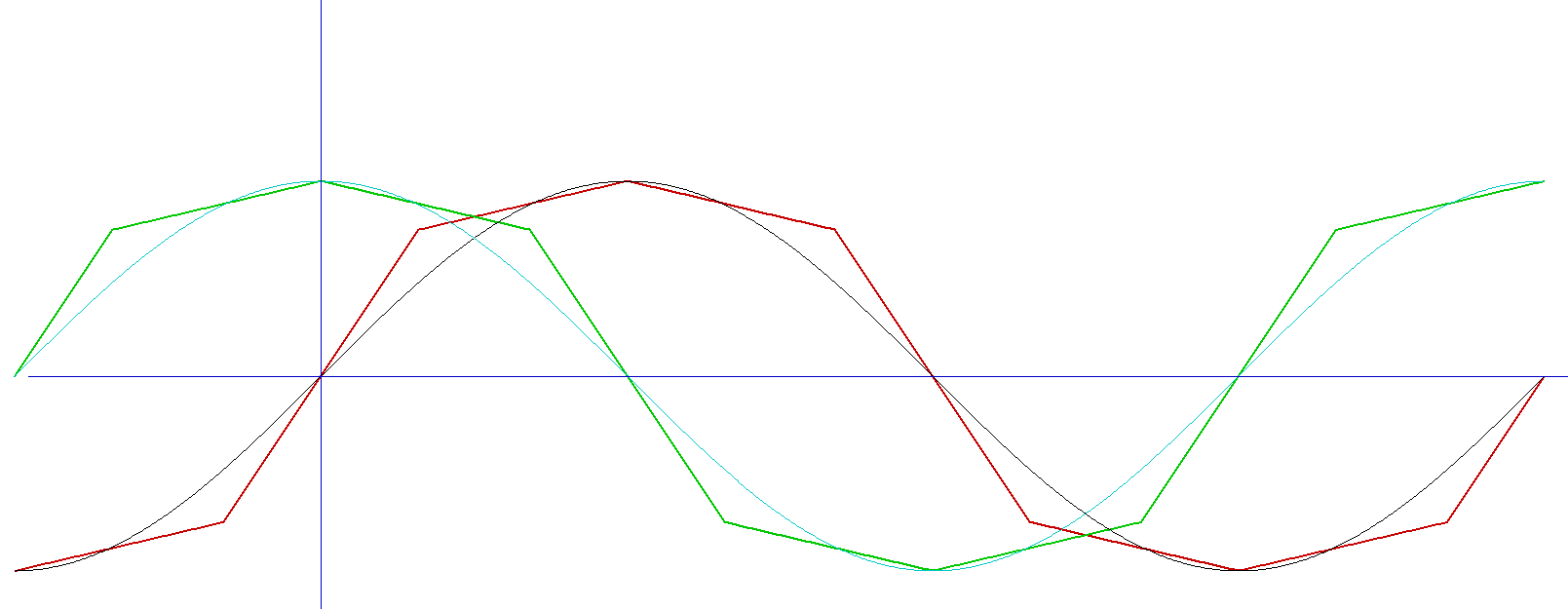
Daraus wird
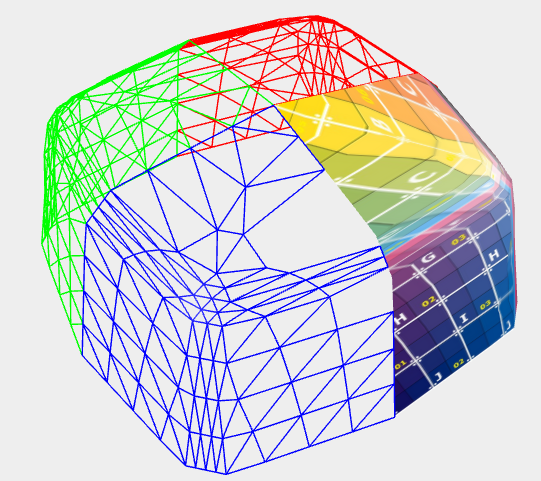
Es ist ein Fehler im 4. (letzten) Oktanten zu erkennen. Offenbar ein nummerisches Problem, muss ich noch näher beleuchten.
Der Code:
XProfan 11
// Periodische Funktion erzeugen
Var px! = 0.5
Var py! = 0.75
//-------------
Window 0,0 - 1800,1000
Var x! = 0
Var y! = 0
Var m! = 0
Var pi2! = Pi() / 2
UsePen 0, 2, RGB(200,0,0)
x! = -1.57
MoveTo 400 + x! * 200 , 500 + 200
WhileLoop 0, 784
x! = x! + 0.01
y! = sinlike(x!)
LineTo 400 + x! * 200 , 500 - y! * 200
EndWhile
UsePen 0, 2, RGB(0,200,0)
x! = -1.57
MoveTo 400 + x! * 200 , 500
WhileLoop 0, 784
x! = x! + 0.01
y! = coslike(x!)
LineTo 400 + x! * 200 , 500 - y! * 200
EndWhile
UsePen 0, 1, RGB(0,0,0)
x! = -1.57
MoveTo 400 + x! * 200 , 500 + 200
WhileLoop 0, 784
x! = x! + 0.01
y! = sin(x!)
LineTo 400 + x! * 200 , 500 - y! * 200
EndWhile
UsePen 0, 1, RGB(0,200,200)
x! = -1.57
MoveTo 400 + x! * 200 , 500
WhileLoop 0, 784
x! = x! + 0.01
y! = cos(x!)
LineTo 400 + x! * 200 , 500 - y! * 200
EndWhile
UsePen 0, 1, RGB(0,0,200)
Line 100, 500, 1700, 500
Line 400, 50, 400, 900
waitinput
Proc k1
Parameters x!
m! = ( 1 - py! ) / ( pi2! - px! )
if x! <= px!
return py! / px! * x!;
endif
if x! > px!
return m! * x! + 1 - pi2! * m!
endif
EndProc
Proc sinlike
Parameters x!
if ( x! < 0 )
return -k1( -x! )
endif
if ( x! >= 0 ) AND ( x! <= pi2!)
return k1( x! );
endif
if ( x! > pi2! ) AND ( x! <= Pi() )
return k1( Pi() - x! );
endif
if ( x! > Pi() ) AND ( x! <= 3 * pi2! )
return -k1( x! - Pi() );
endif
if ( x! > 3 * pi2! ) AND ( x! <= 2 * Pi() )
return -k1( 2 * Pi() - x! );
endif
if ( x! > 2 * Pi() ) AND ( x! <= 5 * pi2!)
return k1( x! - 2 * Pi() );
endif
EndProc
Proc coslike
Parameters x!
return sinlike( x! + pi2! );
EndProc
nur die Funktionen in JavaScript
var px = 0.5;
var py = 0.75;
function k1( x ) {
var m = ( 1 - py ) / ( pi2 - px );
return x > px ? m * x + 1 - pi2 * m : py / px * x;
}
function sinlike( x ) {
if ( x < 0 ) return -k1( -x );
if ( x >= 0 && x <= pi2 ) return k1( x );
if ( x > pi2 && x <= pi ) return k1( pi - x );
if ( x > pi && x <= 3 * pi2 ) return -k1( x - pi );
if ( x > 3 * pi2 && x <= 2 * pi ) return -k1( 2 * pi - x );
if ( x > 2 * pi && x <= 5 * pi2) return k1( x - 2 * pi );
}
function coslike( x ) {
return sinlike( x + pi2 );
}
|
| | | | | | |
| | 
p.specht
 | | | | | XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 07.02.2018 ▲ |
| | |
| | 
HofK | Offenbar ein nummerisches Problem, muss ich noch näher beleuchten.
Schuld sind die unvermeidlichen Rundungsfehler. So kommt es vor, dass 5 mal Pi-Halbe leicht überschritten wird. Abhilfe schafft eine kleine Zugabe oder weglassen der oberen Schranke. Letztere Methode hat den Nachteil, dass dann irgendwelche Folgefehler schwerer zu ermitteln sind.
if ( x > 2 * pi && x <= 5 * pi2 + 0.001 ) return k1( x - 2 * pi, t );
//if ( x > 2 * pi ) return k1( x - 2 * pi, t ); // ???
Neu: Parameter t in der Funktion k1.
Es gibt mittlerweile drei Modi um die Form festzulegen.
g.contourmode mit den möglichen Werten
'rounding'
'profile'
'point'
Bei der Parameterangabe sieht das dann so aus.
var parameters = {
contourmode: 'profile',
// rounding: function( t ){ return -0.7 + 1.2 * ( 1 + Math.sin( 0.4 * t ) ) },
profile: function( x, t ){ return 0.90 * Math.sin( x ) + 0.10 * Math.sin( 9 * x ) * Math.sin( t ) },
// pointX: function( t ){ return 0.6 * ( 1 + Math.sin( 0.4 * t) ) },
// pointY: function( t ){ return 0.4 * ( 1 + Math.sin( 0.3 * t) ) },
}
Bei 'profile' ist eine beliebige Funktion mit f(0,t) = 0 und f(Pi/2,t) = 1 anzugeben.
Diese wird dann wieder periodisch auf 0 bis 2*Pi erweitert.
Ein Schnappschuss des obigen Beispiels
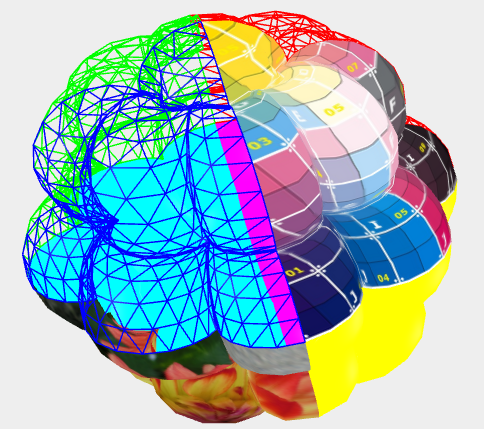 |
| | | | | | |
| | 
HofK | Der Konturmodus 'point' ist ganz schön eckig.
Da gibt es doch noch die Bézierkurven [...]  um die Ecke auszubügeln. Hier benötigt man die quadratische Form der Kurve. um die Ecke auszubügeln. Hier benötigt man die quadratische Form der Kurve.
Allerdings sind die Kurven abhängig von einem Parameter definiert. Ich benötige aber eine Funktion y = f(x). Also muss der Parameter raus. Die äußeren Punkte sind fest: P0(0,0) und P2(Pi/2, 1). Der mittlere Punkt sei P1(px, py)
Durch ( 0, 0 ) vereinfacht sich die Rechnung. Man kann durch lösen einer quadratischen oder linearen Gleichung den Parameter in Abhängigkeit von x ermitteln und dann in die Parametergleichung y einsetzen. Der Parameter t ist hier nicht die Zeit! Da muss man aufpassen, sonst gibt es Chaos. Also mal wieder ein Blatt Papier verbraucht.

Mit XProfan sieht das dann so aus:
// Bezierfunktion 0 .. Pi/2
Var pi2! = Pi() / 2
Var px! = 1.2
Var py! = 0.4
//-------------
Window 0,0 - 1800,1000
Var x! = 0
Var y! = 0
UsePen 0, 1, RGB(0,0,200)
Line 500, 600, 1000, 600
Line 600, 400, 914, 400
Line 600, 300, 600, 700
Line 914, 400, 914, 600
UsePen 0, 3, RGB(200,0,0)
MoveTo 600 , 600
WhileLoop 0, 156
x! = x! + 0.01
y! = bezier( x!, px!, py! )
LineTo 600 + x! * 200 , 600 - y! * 200
EndWhile
waitinput
Proc bezier
Parameters x!// , px!, py!
var tm! = 0
var a! = pi2! - 2 * px!
If a! = 0
tm! = x! / ( 2 * px!)
Else
var tp! = px! / a!
var tr! = tp! * tp! + x! / a!
If ( px! < pi2! / 2)
tm! = -tp! + Sqrt( tr! )
Else
tm! = -tp! - Sqrt( tr! )
Endif
Endif
return ( 1 - 2 * py!) * tm! * tm! + 2 * py! * tm!
EndProc
Mit Strichstärke 3:
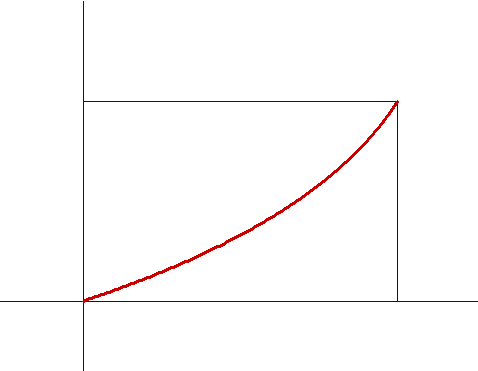
In JavaScript:
Da auch hier ein Punkt anzugeben ist, habe ich contourmode nochmal geändert. Jetzt gibt es 'rounding' 'profile' 'bezier' 'linear'
(linear war vorher point)
Noch zwei Schnappschüsse bei zeitabhängigen Punkten (t Zeit)
contourmode: 'bezier',
pointX: function( t ){ return 0.6 * ( 1 + Math.sin( 0.4 * t) ) },
pointY: function( t ){ return 0.4 * ( 1 + Math.sin( 0.3 * t) ) },
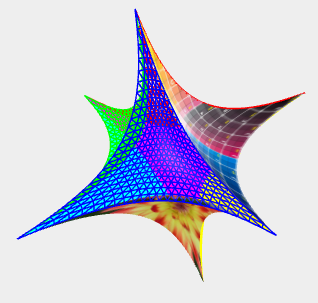
 |
| | | | | | |
| | 
HofK |  geschafft geschafft 
Die erste spezielle Geometrie ist soweit fertig. Möglich, dass mir noch eine Ergänzung einfällt, dann wird halt erweitert.
Bei threejs.hofk.de habe ich es eingebunden. Unmittelbarer unter [...]  bzw. [...] bzw. [...]  erreichbar. erreichbar.
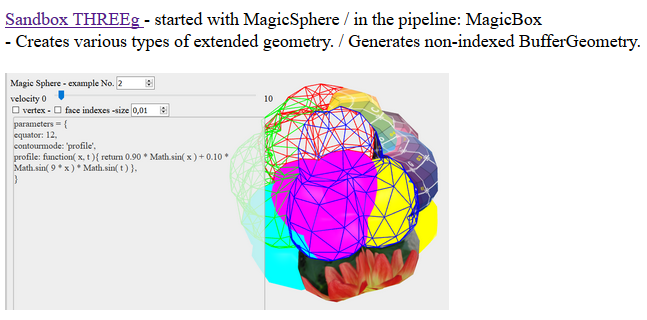
Bei den speziellen Geometrien ist es kein echter Buddelkasten. Es gibt eine beliebig erweiterbare Anzahl von Beispielen mit den zugehörigen Parametern. Das macht Sinn, da die Anzahl der Parameter deutlich geringer ist als bei THREEf und THREEp.
Man kopiert die Parameter einfach in sein eigenes Programm oder ergänzt die Beispielsammlung für sich.
Benutzt man Firefox, bekommt man auch lokal ohne irgendwelche Manipulationen die Texturen.
...
parameterExamples[ 12 ] = {
equator: 30,
uvmode: 1,
contourmode: 'profile',
parts: [ 1, 0, 1, 0, 1, 0, 1, 0 ],
profile: function( x, t ){ return 1 - 0.97* Math.cos( x ) - 0.03 * Math.cos( 21 * x ) },
}
parameterExamples[ 13 ] = {
}
...
Einfach weitere parameterExamples[ ... ] Blöcke ergänzen und ausfüllen.
Die Parameter sind in THREEg.js ersichtlich.
/* parameter overview --- all parameters are optional ---
p = {
// simple properties
equator,
uvmode,
contourmode,
// array, value 1 for octant, otherwise arbitrary - upper counterclockwise, lower clockwise
parts,
// functions with parameter time // function ( t )
radius,
rounding,
profile, // y = f( x, t ), 0 < x < PI / 2, 0 < y < 1
pointX, // interval 0 to PI / 2
pointY, // interval 0 to 1
driftX,
driftY,
driftZ,
explod, // factor for exploded view - non indexed BufferGeometry
}
*/
//............................................................set defaults
g.equator = p.equator !== undefined ? p.equator : 6;
g.uvmode = p.uvmode !== undefined ? p.uvmode : 0;
g.contourmode = p.contourmode !== undefined ? p.contourmode :'rounding'; // 'profile' 'bezier' 'linear'
g.parts = p.parts !== undefined ? p.parts : [ 1, 1, 1, 1, 1, 1, 1, 1 ];
g.radius = p.radius !== undefined ? p.radius : function ( t ) { return 1 };
g.rounding = p.rounding !== undefined ? p.rounding : function ( t ) { return 1 };
g.profile = p.profile !== undefined ? p.profile : function ( x, t ) { return Math.sin( x ) };
g.pointX = p.pointX !== undefined ? p.pointX : function ( t ) { return 0.001 };
g.pointY = p.pointY !== undefined ? p.pointY : function ( t ) { return 0.999 };
g.driftX = p.driftX !== undefined ? p.driftX : function ( t ) { return 0 };
g.driftY = p.driftY !== undefined ? p.driftY : function ( t ) { return 0 };
g.driftZ = p.driftZ !== undefined ? p.driftZ : function ( t ) { return 0 };
g.explode = p.explode !== undefined ? p.explode : function ( t ) { return 0 };
|
| | | | | | |
| | 
p.specht
 | Hah! Die Pixar Studios bekommen offenbar Konkurrenz!
Faszinierend! |
| | | | XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 14.02.2018 ▲ |
| | |
| | 
HofK | Bevor die magische Box dran ist, habe ich einen Abstecher zu den Gitternetzen gemacht. Hat sich so ergeben.

Das Resultat kann dort [...]  genauer betrachtet werden. Rein und raus zoomen. genauer betrachtet werden. Rein und raus zoomen.
Einige Beispiele benötigen meine Addons THREEf, THREEp, THREEg.
Ein Beispiel nutzt eine Erweiterung .toGrid von prisoner849 (Paul West), siehe [...]  und Quellcode hier. und Quellcode hier.
Der Quelltext:
<!DOCTYPE html>
<!-- *** grids ***
/**
* @author hofk
*/
-->
<html lang="de">
<head>
<title> grids </title>
<meta charset="utf-8" />
</head>
<body> </body>
<script src="three.min.89.js"></script>
<script src="OrbitControls.js"></script>
<script src="THREEx.WindowResize.js"></script>
<script src="THREEf.js"></script>
<script src="THREEp.js"></script>
<script src="THREEg.js"></script>
<script>
'use strict'
var scene = new THREE.Scene();
var camera = new THREE.PerspectiveCamera( 75, window.innerWidth / window.innerHeight, 0.1, 2000 );
camera.position.z = 120;
var renderer = new THREE.WebGLRenderer( { antialias: true } );
renderer.setSize( window.innerWidth, window.innerHeight );
renderer.setClearColor( 0x777777, 1 );
var container = document.createElement('div' );
document.body.appendChild( container );
container.appendChild( renderer.domElement );
THREEx.WindowResize( renderer, camera );
var controls = new THREE.OrbitControls( camera, renderer.domElement );
var uvTex = new THREE.TextureLoader().load( "sunflower.png" );// free
var material = new THREE.MeshBasicMaterial( { map: uvTex, side: THREE.DoubleSide} );// not wireframe
var wireMaterial = new THREE.MeshBasicMaterial( { map: uvTex, side: THREE.DoubleSide, wireframe: true } );
function createObliqueGrid( width, height, widthSegments, heightSegments, stretch, flat ) {
width = width !== undefined ? width : 100;
height = height !== undefined ? height : 100;
widthSegments = widthSegments !== undefined ? widthSegments : 20;
heightSegments = heightSegments !== undefined ? heightSegments : 20;
stretch = stretch !== undefined ? stretch : 0;// normally -1 to +1
flat = flat !== undefined ? flat : false;
var split = flat ? 3 : 2;
var halfWidth = width / 2;
var halfHeight = height / 2;
var wp = split * widthSegments + 1;
var dwp = width / widthSegments / split;
var dhp = height / heightSegments / 2;
var st = 1 + stretch;
var obliqueGrid = new THREE.Object3D( );
var zigzags = [ ];
var geometryZigzag = [ ];
var positions = [ ];
var uvs = [ ];
var sign, i1;
for ( var i = 0; i < heightSegments * 2; i ++ ) {
geometryZigzag[ i ] = new THREE.BufferGeometry();
positions[ i ] = new Float32Array( wp * 3 );
uvs[ i ] = new Float32Array( wp * 2 );
geometryZigzag[ i ].addAttribute('position', new THREE.BufferAttribute( positions[ i ], 3 ) );
geometryZigzag[ i ].addAttribute('uv', new THREE.BufferAttribute( uvs[ i ], 2 ) );
sign = i % 2 === 0 ? -1 : 1;
i1 = i % 2 === 0 ? i + 1 : i;
for ( var j = 0; j < wp ; j ++ ) {
positions[ i ][ j * 3 ] = j * dwp;
positions[ i ][ j * 3 + 1 ] = j % split === 0 ? 0 : sign * st * dhp;
positions[ i ][ j * 3 + 2 ] = 0;
}
zigzags[ i ] = new THREE.Line( geometryZigzag[ i ], material );// material is not wireframe - still a grid
for ( var j = 0; j < wp ; j ++ ) {
zigzags[ i ].geometry.getAttribute('uv' ).array[ j * 2 ] = j * dwp / width;
zigzags[ i ].geometry.getAttribute('uv' ).array[ j * 2 + 1 ] = ( i1 * dhp + ( j % split === 0 ? 0 : sign * st * dhp ) ) / height;
}
zigzags[ i ].position.set( -halfWidth, i1 * dhp - halfHeight, 0 );
obliqueGrid.add( zigzags[ i ] );
}
return obliqueGrid;
}
function createHexagonGrid( radius, rings ) {
// outer grid radius, rings of hexagons around the central hexagon
radius = radius !== undefined ? radius : 50;
rings = rings !== undefined ? rings : 20;
var x, y;
var r = 2 * radius / ( 2 * rings + 1 ) / Math.sqrt( 3 );// radius of corner points, size of a single hexagon
var ri = r * Math.sqrt( 3 ) / 2;// inner radius of a single hexagon
var pi6 = Math.PI / 6;
var hexagonGrid = new THREE.Object3D( );
var hexagons = [ ];
//var hexagonCount = 3 * rings * rings + 3 * rings + 1;
var geometryHexagon = [ ];
var positions = [ ];
var uvs = [ ];
var h = 0;
for ( var sg = -1; sg < 2; sg ++ ) {
var rg0 = sg === 0 ? rings : 0;
for( var i = 1, k = 2 * rings + 1 - Math.abs( sg ); k > rings + rg0; i ++, k -- ) {
x = ri * ( 1 - k );
y = sg * 1.5 * r * i;
for( var j = 0 ; j < k; j ++ ) {
geometryHexagon[ h ] = new THREE.BufferGeometry();
positions[ h ] = new Float32Array( 18 );
uvs[ h ] = new Float32Array( 12 );
geometryHexagon[ h ].addAttribute('position', new THREE.BufferAttribute( positions[ h ], 3 ) );
geometryHexagon[ h ].addAttribute('uv', new THREE.BufferAttribute( uvs[ h ], 2 ) );
for( var ip = 0; ip < 6; ip ++ ) {
positions[ h ][ ip * 3 ] = r * Math.cos( ( 2 * ip + 1 ) * pi6 );
positions[ h ][ ip * 3 + 1 ] = r * Math.sin( ( 2 * ip + 1 ) * pi6 );
positions[ h ][ ip * 3 + 2 ] = 0;
}
hexagons[ h ] = new THREE.LineLoop( geometryHexagon[ h ], material );// material is not wireframe - still a grid
for( var iuv = 0; iuv < 6; iuv ++ ) {
hexagons[ h ].geometry.getAttribute('uv' ).array[ iuv * 2 ] = 0.5 * ( 1 + ( x + r * Math.cos( ( 2 * iuv + 1 ) * pi6 ) ) / radius );
hexagons[ h ].geometry.getAttribute('uv' ).array[ iuv * 2 + 1 ] = 0.5 * ( 1 + ( y + r * Math.cos( ( 2 * iuv + 1 ) * pi6 ) ) / radius );
}
x += ri * 2;
hexagons[ h ].position.set( x, y, 0 );
hexagonGrid.add( hexagons[ h ] );
h ++;
}
}
}
return hexagonGrid;
}
/* .toGrid: function() from prisoner849 (Paul West)
https://discourse.threejs.org/t/gridboxgeometry/1420
https://discourse.threejs.org/t/grids-of-waves-shaders/1168
https://jsfiddle.net/prisoner849/mcdtatpv/
*/
Object.assign(THREE.PlaneBufferGeometry.prototype, {
toGrid: function() {
let segmentsX = this.parameters.widthSegments || 1;
let segmentsY = this.parameters.heightSegments || 1;
let indices = [];
for (let i = 0; i < segmentsY + 1; i++) {
let index11 = 0;
let index12 = 0;
for (let j = 0; j < segmentsX; j++) {
index11 = (segmentsX + 1) * i + j;
index12 = index11 + 1;
let index21 = index11;
let index22 = index11 + (segmentsX + 1);
indices.push(index11, index12);
if (index22 < ((segmentsX + 1) * (segmentsY + 1) - 1)) {
indices.push(index21, index22);
}
}
if ((index12 + segmentsX + 1) <= ((segmentsX + 1) * (segmentsY + 1) - 1)) {
indices.push(index12, index12 + segmentsX + 1);
}
}
this.setIndex(indices);
return this;
}
});
var geometry = new THREE.PlaneBufferGeometry( 40, 40, 40, 40 );
var geometryTHREEf = new THREE.BufferGeometry();
geometryTHREEf.createMorphGeometry = THREEf.createMorphGeometry;
geometryTHREEf.createMorphGeometry({
style:'map',
radius: 6.5,
height: 40,
radiusSegments: 20,
heightSegments: 20,
waffled: true,
});
var rhombGeometry = new THREE.PlaneBufferGeometry( 40, 40, 40, 40 );
var toGridGeometry = new THREE.PlaneBufferGeometry( 40, 40, 40, 40 ).toGrid();// .toGrid() from prisoner849 (Paul West)
var geometryTHREEp3 = new THREE.BufferGeometry();
geometryTHREEp3.createMorphGeometry = THREEp.createMorphGeometry;
geometryTHREEp3.createMorphGeometry({
style:'map',
radius: 12,
wedges: 3,
usedWedges: 3,
equator: 20,
bottom: 20,
top: 40,
});
var geometryTHREEg = new THREE.BufferGeometry();
geometryTHREEg.createMagicSphere = THREEg.createMagicSphere;
geometryTHREEg.createMagicSphere({
rounding: function ( t ) { return 0 },
radius: function ( t ) { return 30 },
equator: 40,
parts: [ 1 ],
});
var geometryTHREEp = new THREE.BufferGeometry();
geometryTHREEp.createMorphGeometry = THREEp.createMorphGeometry;
geometryTHREEp.createMorphGeometry({
style:'map',
radius: 12,
equator: 20,
bottom: 20,
top: 40,
});
// ...........................................................
var mesh0 = new THREE.Mesh( geometry, material );// material is not wireframe - no grid
scene.add( mesh0 );
mesh0.position.set( -100, 50, 0 );
var obliqueGrid = new createObliqueGrid( 40, 40, 40, 40, 0.4, true );
scene.add( obliqueGrid );
obliqueGrid.position.set( -50, 50, 0 );
var hexagonGrid = createHexagonGrid( 20, 25 );// grid radius and rings of hexagons around the central hexagon
scene.add( hexagonGrid );
hexagonGrid.position.y = 50;
var meshTHREEf = new THREE.Mesh( geometryTHREEf, wireMaterial );
scene.add( meshTHREEf );
meshTHREEf.position.set( 30, 50, 0 );
var mesh1 = new THREE.Mesh( geometry, wireMaterial );
scene.add( mesh1 );
mesh1.position.x = -50;
var rhombMesh = new THREE.LineSegments( rhombGeometry, material );// material is not wireframe - still a grid
scene.add( rhombMesh );
var gridMesh = new THREE.LineSegments( toGridGeometry, material );// material is not wireframe - still a grid
scene.add( gridMesh );
gridMesh.position.x = 50;
var meshTHREEp3 = new THREE.Mesh( geometryTHREEp3, wireMaterial );
scene.add( meshTHREEp3 );
meshTHREEp3.position.set( -70, -50, 0 );
meshTHREEp3.rotation.set( 1.57, 1.57, 0 );
var meshTHREEg = new THREE.Mesh( geometryTHREEg, wireMaterial );
scene.add( meshTHREEg );
meshTHREEg.position.set( 0, -57, -20 );
meshTHREEg .rotation.set( 0.62, -2.35, 0 );
var meshTHREEp = new THREE.Mesh( geometryTHREEp, wireMaterial );
scene.add( meshTHREEp );
meshTHREEp.position.set( 30, -50, 0 );
meshTHREEp.rotation.set( 1.57, 1.57, 0 );
var gridHelper = new THREE.GridHelper( 150, 3, 0x00ff00, 0x00ff00 );
scene.add( gridHelper );
gridHelper.rotation.x = 1.57
animate();
function animate() {
requestAnimationFrame( animate );
renderer.render( scene, camera );
controls.update();
}
</script>
</html>
|
| | | | | | |
| | 
HofK | Eigentlich muss man für die magische Box nur die Grundkonstruktion von THREEf nehmen. Der Style 'map' liefert ein Rechteck. Davon benötigt man sechs für die Seiten und dann noch 12 für die abgerundeten Kanten. Die Abrundung ist ähnlich wie bei der magischen Kugel aus THREEg zu bewerkstelligen, da diese Konstruktion die 8 Ecken liefert und die insgesamt 26 Teile der Box zusammenpassen sollen.
Also habe ich fleißig zusammen kopiert. Das Problem sind sich eventuell überschneidende Bezeichnungen und die Gesamtstruktur. Da kann man nicht immer nur kopieren sondern muss abwandeln und anpassen.
Mittlerweile funktioniert das Grundgerüst. Die Ecken habe ich zum Test etwas heraus gesetzt. Die 12 Kantenteile müssen noch positioniert und gebogen werden, auf dem Bild ist nur eine ebene Testkante.
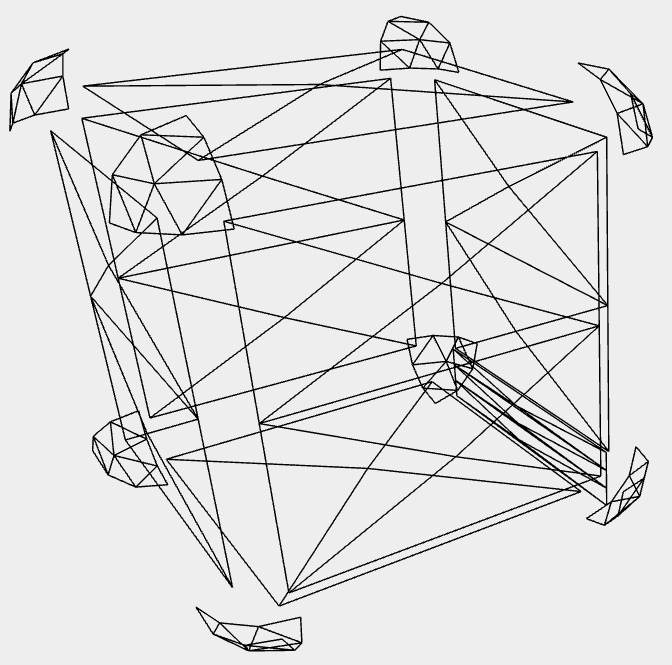
Man kann wählen, welche Teile dargestellt werden sollen. Default für das seitenbezogene Datenfeld ist [ 1, 1, 1, 1, 1, 1 ]
// array, sides order +x, -x, +y, -y, +z, -z
sides,// values: no side = 0, complete = 1, in addition: no plane = 2, edgeless = 3, no corners = 4
Dabei gilt die Eigenschaft "nicht darstellen" für die der Seite zugeordneten Teile. Wählt man also 4 für die ersten beiden Elemente das Feldes, wird bereits keine Ecke dargestellt. Die Seiten liegen gegenüber und betreffen damit alle 8 Ecken.
Mit den vorbereitenden Funktionen werden bis zu 26 Teile erzeugt.
Ähnlich dann beim Morphen. Auch die Box ist nicht nur statisch. |
| | | | | | |
| | 
HofK | | | | | | | |
| | 
ByteAttack | Zu kompliziert für mich  Bin raus Bin raus  |
| | | | | | |
| | 
p.specht
 | | Beim scrollen der Seite entsteht der Eindruck, dass die untere Biegung der Figur etwas nachhinkt im Bildaufbau... könnte eine optische Täuschung sein. Sonst: Toll ! |
| | | | XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 01.03.2018 ▲ |
| | |
|
AntwortenThemenoptionen | 391.116 Betrachtungen |
ThemeninformationenDieses Thema hat 10 Teilnehmer: |