PHP, HTML & JavaScript- Forum | | | | | | - Seite 1 - |
| 
HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
| | | | | | |
| | | | | | - Seite 23 - |
| | 
HofK | 
Es entwickelt sich.
Noch längst nicht fehlerfrei, da bisher nur das Grundverfahren ohne notwendige Prüfungen und Korrekturen für extreme Fälle implementiert sind. Locker geschriebene 400 Zeilen Code mit vielen console.log() Statements zur Kontrolle. |
| | | | | | |
| | 
HofK | Der erste Schritt ist geschafft.
Eine einfache Kugel.
Allein dafür braucht man das Verfahren nicht, da es genug andere Möglichkeiten gibt. Aber es ist die Basis von der man ausgehen kann um nun beliebige Öffnungen in die Kugel und andere Körper zu bekommen.
Nicht nur kreisförmige Öffnungen!
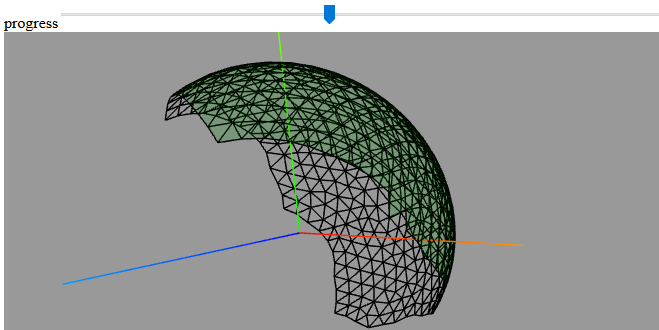
Dort ist die Kugel zu finden: [...] 
Die Berechnung/ Darstellung erfolgt so schnell, dass man den Fortschritt
nicht verfolgen kann. Deshalb habe ich die Möglichkeit vorgesehen den
Ablauf mittels Schieber zu verfolgen. Im Test ergab sich die kleinste
sinnvolle Variante mit detail = 10. In der vorliegenden Form bis 40 möglich.
Das Verfahren von Prof. E. Hartmann [...]  Seite 47 wurde für den speziellen Fall der Kugel abgeändert / vereinfacht. Die Berechnung der Frontwinkel erfolgt nach einem alternativen Verfahren. Seite 47 wurde für den speziellen Fall der Kugel abgeändert / vereinfacht. Die Berechnung der Frontwinkel erfolgt nach einem alternativen Verfahren.
Der Code:
( HINWEIS: Die Formatierung hier hat Probleme mit if ( start ) start = false; ohne geschweifte Klammer! Die Klammer } gehört zum while. Die Einrückung stimmt dann nicht mehr.)
<!DOCTYPE html>
<!-- -->
<head>
<title> TriangulationSphere </title>
<meta charset="utf-8" />
</head>
<body>
progress<input type="range" id="range" min="0" max="300" value="150" step="0.2" style="width: 80%;">
</body>
<script src="../js/three.min.105.js"></script>
<script src="../js/OrbitControls.js"></script>
<script>
// @author hofk
// Algorithmus nach / Algorithm based on
// de: https://www2.mathematik.tu-darmstadt.de/~ehartmann/cdg0/cdg0n.pdf
// en: https://www2.mathematik.tu-darmstadt.de/~ehartmann/cdgen0104.pdf
'use strict'
let scene = new THREE.Scene();
let camera = new THREE.PerspectiveCamera( 55, window.innerWidth / window.innerHeight, 0.1, 100 );
camera.position.set( 1, 2, 3 );
let renderer = new THREE.WebGLRenderer( { antialias: true } );
renderer.setSize( window.innerWidth, window.innerHeight );
renderer.setClearColor( 0x999999, 1 );
let container = document.createElement('div' );
document.body.appendChild( container );
container.appendChild( renderer.domElement );
const controls = new THREE.OrbitControls( camera, renderer.domElement );
const axesHelper = new THREE.AxesHelper( 1.5 );
scene.add( axesHelper );
// ....................................
const g = new THREE.BufferGeometry( );
//g.setDrawRange ( 0, 0 );
let detail = 25;
sphere( g, detail );
//.....................................
let material1 = new THREE.MeshBasicMaterial( { side: THREE.DoubleSide, color: 0x000000, wireframe: true } );
let mesh1 = new THREE.Mesh( g, material1 );
scene.add( mesh1 );
let material2 = new THREE.MeshBasicMaterial( { side: THREE.FrontSide, color: 0x008800, transparent: true, opacity: 0.2 } );
let mesh2 = new THREE.Mesh( g, material2 );
scene.add( mesh2 );
animate( );
// ....................................
function animate( ) {
g.setDrawRange ( 0, range.value * detail );
requestAnimationFrame( animate );
renderer.render( scene, camera );
controls.update( );
}
// ....................................
function sphere( g, detail ) {
const length = ( x, y, z ) => ( Math.sqrt( x * x + y * y + z * z ) );
const prevFront = ( i ) => ( i !== 0 ? i - 1 : front.length - 1 );
const nextFront = ( i ) => ( i !== front.length - 1 ? i + 1 : 0 );
let m, n, nT, dAng, len, d, d1, d2, d12, dd1, dd2, dd12, centerAngle, h, acute, concave, posIdx, indIdx, frontPosIdx;
// points and vectors:
let x, y, z, xp, yp, zp, xc, yc, zc, x1, y1, z1, x2, y2, z2, xt1, yt1, zt1, xt2, yt2, zt2, xv1, yv1, zv1, xv2, yv2, zv2;
// preparation
const posCount = detail * 100;
const faceCount = detail * 150;
g.indices = new Uint32Array( faceCount * 3 );
g.positions = new Float32Array( posCount * 3 );
//g.normals = new Float32Array( posCount * 3 );
g.setIndex( new THREE.BufferAttribute( g.indices, 1 ) );
g.addAttribute('position', new THREE.BufferAttribute( g.positions, 3 ) );
d = Math.PI / detail;// rough side length of the triangles
posIdx = 0;
indIdx = 0;
// first triangle
storePoint( 0, 0 );// ( theta, phi )
storePoint( d, -detail / 6 * d );
storePoint( d, detail / 6 * d );
g.indices[ 0 ] = 0;
g.indices[ 1 ] = 1;
g.indices[ 2 ] = 2;
indIdx += 3;
let front = [];
front.push( { idx: 0, ang: 0, chg: true }, { idx: 1, ang: 0, chg: true }, { idx: 2, ang: 0, chg: true } );
let fLen;// front polygone length
let start = true;
// ------ triangulation cycle -------------
while ( front.length > 3 || start ) {
if ( start ) start = false;
calculateFrontAngles( );
m = getMinimalAngleIndex( );// front angle
newTriangles( m );
}
// last triangle
g.indices[ indIdx ] = front[ 2 ].idx;
g.indices[ indIdx + 1 ] = front[ 1 ].idx
g.indices[ indIdx + 2 ] = front[ 0 ].idx;
// ..... main detail functions .....
function calculateFrontAngles( ) {
for ( let i = 0; i < front.length; i ++ ) {
if( front[ i ].chg ) {
getPrevPoint( i );// (1)
getPoint( i );
getNextPoint( i );// (2)
xv1 = xp - x1;
yv1 = yp - y1;
zv1 = zp - z1;
len = length( xv1, yv1, zv1 );// to normalize
xv1 = xv1 / len;
yv1 = yv1 / len;
zv1 = zv1 / len;
xv2 = x2 - xp;
yv2 = y2 - yp;
zv2 = z2 - zp;
len = length( xv2, yv2, zv2 );// to normalize
xv2 = xv2 / len;
yv2 = yv2 / len;
zv2 = zv2 / len;
front[ i ].ang = Math.acos( Math.abs( xv1 * xv2 + yv1 * yv2 + zv1 * zv2 ) );
// cross, to detect curvature
x = yv1 * zv2 - zv1 * yv2;
y = zv1 * xv2 - xv1 * zv2;
z = xv1 * yv2 - yv1 * xv2;
len = length( x, y, z );// to normalize
x = xp + x / len;
y = yp + y / len;
z = zp + z / len;
concave = ( length( x, y, z ) < Math.sqrt( 2 ) );
d1 = length( x1 - xp, y1 - yp, z1 - zp );
d2 = length( x2 - xp, y2 - yp, z2 - zp );
d12 = length( x2 - x1, y2 - y1, z2 - z1 );
dd1 = d1 * d1;
dd2 = d2 * d2;
dd12 = d12 * d12;
acute = ( dd12 < ( dd1 + dd2) );
// if ( concave && acute ) front[ i ].ang += 0;
if ( concave && !acute ) front[ i ].ang = Math.PI - front[ i ].ang ;
if ( !concave && acute ) front[ i ].ang = 2 * Math.PI - front[ i ].ang ;
if ( !concave && !acute ) front[ i ].ang = Math.PI + front[ i ].ang ;
front[ i ].chg = false;
}
}
}
function getMinimalAngleIndex( ) {
let angle = Infinity;
let m;
for ( let i = 0; i < front.length; i ++ ) {
if( front[ i ].ang < angle ) {
angle = front[ i ].ang ;
m = i;
}
}
return m;
}
function newTriangles( m ) {
// m: minimal angle (index)
let frNew = [];// new front points
nT = Math.floor( 3 * front[ m ].ang / Math.PI ) + 1;// number of new triangles
dAng = front[ m ].ang / nT;
getSystemAtPoint( m );
getNextPoint( m );
d1 = length( x1 - xp, y1 - yp, z1 - zp );
d2 = length( x2 - xp, y2 - yp, z2 - zp );
d12 = length( x2 - x1, y2 - y1, z2 - z1 );
// correction of dAng, nT in extreme cases
if ( dAng < 0.8 && nT > 1 ) {
nT --;
dAng = front[ m ].ang / nT;
}
if ( dAng > 0.8 && nT === 1 && d12 > 1.25 * d ) {
nT = 2;
dAng = front[ m ].ang / nT;
}
if ( d1 * d1 < 0.2 * d * d || d2 * d2 < 0.2 * d * d ) {
nT = 1;
}
n = nT - 1;// n number of new points
if ( n === 0 ) {// one triangle
g.indices[ indIdx ] = front[ m ].idx;
g.indices[ indIdx + 1 ] = front[ prevFront( m ) ].idx;
g.indices[ indIdx + 2 ] = front[ nextFront( m ) ].idx;
indIdx += 3;
front[ prevFront( m ) ].ang = 0;
front[ prevFront( m ) ].chg = true;
front[ nextFront( m ) ].ang = 0;
front[ nextFront( m ) ].chg = true;
front.splice( m, 1 );// delete point with index m from the front
} else {// more then one triangle
for ( let i = 0, phi = dAng; i < n; i ++, phi += dAng ) {
xp = xc + Math.cos( phi ) * d * xt1 + Math.sin( phi ) * d * xt2;
yp = yc + Math.cos( phi ) * d * yt1 + Math.sin( phi ) * d * yt2;
zp = zc + Math.cos( phi ) * d * zt1 + Math.sin( phi ) * d * zt2;
len = length( xp, yp, zp );// to normalize
g.positions[ posIdx ] = xp / len;
g.positions[ posIdx + 1 ] = yp / len;
g.positions[ posIdx + 2 ] = zp / len;
frNew.push( { idx: posIdx / 3, ang: 0, chg: true } );
posIdx += 3;
}
g.indices[ indIdx ] = front[ m ].idx;
g.indices[ indIdx + 1 ] = front[ prevFront( m ) ].idx
g.indices[ indIdx + 2 ] = frNew[ 0 ].idx;
indIdx += 3;
front[ prevFront( m ) ].ang = 0;
front[ prevFront( m ) ].chg = true;
for ( let i = 0; i < n - 1; i ++ ) {
g.indices[ indIdx ] = front[ m ].idx;
g.indices[ indIdx + 1 ] = frNew[ i ].idx;
g.indices[ indIdx + 2 ] = frNew[ i + 1 ].idx;
indIdx += 3;
}
g.indices[ indIdx ] = front[ m ].idx;
g.indices[ indIdx + 1 ] = frNew[ n - 1 ].idx;
g.indices[ indIdx + 2 ] = front[ nextFront( m ) ].idx;
front[ nextFront( m ) ].ang = 0;
front[ nextFront( m ) ].chg = true;
indIdx += 3;
replaceFront( m, insertFront );// replaces front[ m ] with new points
}
}
// ..... help functions .....
function replaceFront( m, fNew ) {
let rear = front.splice( m, front.length - m )
for ( let i = 0; i < fNew.length; i ++ ) {
front.push( fNew[ i ] );// new front points
}
for ( let i = 1; i < rear.length; i ++ ) {// 1: without old front point m
front.push( rear[ i ] );
}
}
function getSystemAtPoint( i ) {
getPrevPoint( i );
getPoint( i );
// centerAngle = Math.acos( Math.abs( x1 * xp + y1 * yp + z1 * zp ) );
// r = Math.sin( centerAngle ); // radius cutting circle
// h = Math.cos( centerAngle ); // distance center to cutting circle
h = Math.abs( x1 * xp + y1 * yp + z1 * zp );
// center cutting circle (refers to previous point)
xc = h * xp;
yc = h * yp;
zc = h * zp;
// first tangent
xt1 = x1 - xc;
yt1 = y1 - yc;
zt1 = z1 - zc;
len = length( xt1, yt1, zt1 );// to normalize
xt1 = xt1 / len;
yt1 = yt1 / len;
zt1 = zt1 / len;
// cross, second tangent (sphere radius 1: p equals normal)
xt2 = yp * zt1 - zp * yt1;
yt2 = zp * xt1 - xp * zt1;
zt2 = xp * yt1 - yp * xt1;
}
function getPrevPoint( i ) {
frontPosIdx = front[ prevFront( i ) ].idx * 3 ;
x1 = g.positions[ frontPosIdx ];
y1 = g.positions[ frontPosIdx + 1 ];
z1 = g.positions[ frontPosIdx + 2 ];
}
function getPoint( i ) {
frontPosIdx = front[ i ].idx * 3;
xp = g.positions[ frontPosIdx ];
yp = g.positions[ frontPosIdx + 1 ];
zp = g.positions[ frontPosIdx + 2 ];
}
function getNextPoint( i ) {
frontPosIdx = front[ nextFront( i ) ].idx * 3;
x2 = g.positions[ frontPosIdx ];
y2 = g.positions[ frontPosIdx + 1 ];
z2 = g.positions[ frontPosIdx + 2 ];
}
function storePoint( theta, phi ) {
g.positions[ posIdx ] = Math.sin( theta ) * Math.cos( phi );
g.positions[ posIdx + 1 ] = Math.cos( theta );
g.positions[ posIdx + 2 ] = -Math.sin( theta ) * Math.sin( phi );
posIdx += 3;
}
}
</script>
</html>
UPDATES: 19.06. / 26.06. / 07.07. Bugfix / Optimierung im Code |
| | | | | | |
| | 
HofK | Fast geschafft! 

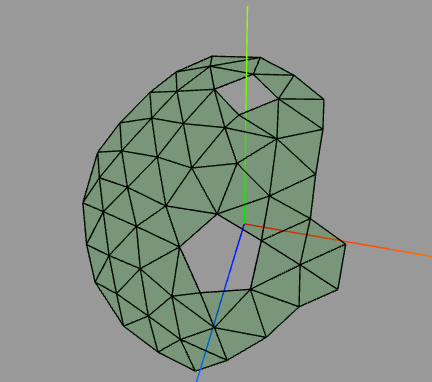
Eine Kugel mit zwei nach Bedarf angeordneten Öffnungen.
Das Verfahren ist noch nicht bis in das letzte Detail umgesetzt. Dadurch ergeben sich bei einigen Versuchen fehlerhafte Triangulierungen.
Unter
6.1.6 Der Schritt S2 [...] 
"Um zu verhindern, daß neue Dreiecke alte Dreiecke überdecken, prüfen wir ...
• den Abstand der Punkte des aktuellen Frontpolygons Π0 zu Punkten aller restlichen Frontpolygone ...
Die Punkte p0i und pmj erscheinen zweimal ! Deshalb sollte man als nächtes die Frontwinkel dieser Punkte bei ihrem ersten Erscheinen im Polygon Π0 bestimmen und zuerst den Punkt vervollständigen (mit Dreiecken umgeben, s. Schritt S3), der den kleinsten Winkel besitzt, und dann den zweiten (s. 6.9e). Danach wird das erste Erscheinen dieser beiden Punkte aus dem aktuellen Frontpolygon gestrichen. p0i,pmj dürfen bei späteren Abstandsprüfungen nicht mehr verwendet werden."
Noch bin ich am überlegen und testen, wie ich diese Sonderanforderungen möglichst elegant und effektiv in die schon vorhandene Programmstruktur einbinde. Eventuell muss ich auch in der Struktur des Scripts dazu Änderungen machen. |
| | | | | | |
| | 
HofK | Es scheint zu funktionieren.
Eine Kugel mit vielen Löchern:
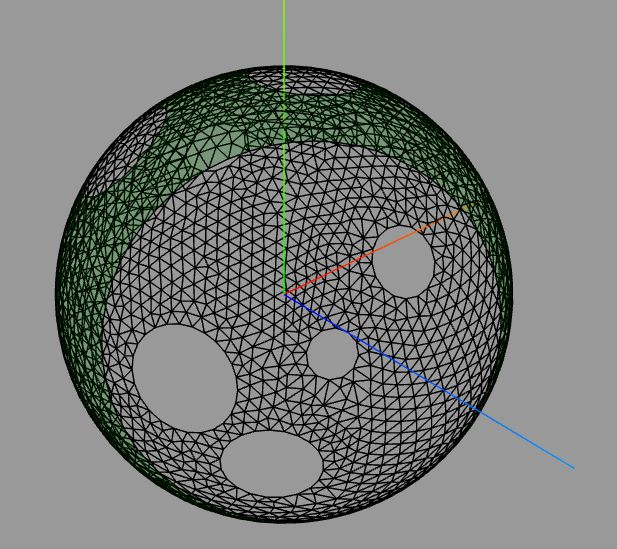
So habe ich die Extras realisiert.
Was noch nicht geht:
Zwei sich überschneidende Lochkreise bzw. andere sich überschneidende Öffnungen. |
| | | | | | |
| | 
HofK | Noch hinbekommen.
Kreisförmiges und frei definiertes Loch:
Darstellung bei teilweiser Triangulierung.

... noch ohne Überschneidung. |
| | | | | | |
| | 
p.specht
 | Einfach toll, was schon geht - zumindest bei starken Rechnern!
Gruss |
| | | | XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 17.06.2019 ▲ |
| | |
| | 
HofK | ... bei mir läuft das "wie geschmiert Brot" - in die Jahre gekommene Technik siehe weiter oben.
Auch solche Öffnungen sind machbar.
 |
| | | | | | |
| | 
p.specht
 | Nur so als Anregung, in welche Richtung es gehen könnte: [...]  |
| | | | XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 21.06.2019 ▲ |
| | |
| | 
HofK | Erstmal ein "fertige" Version der Kugel mit beliebigen Öffnungen.
Dort gepostet: [...] 
Dort gleich ausprobieren: [...]  |
| | | | | | |
| | 
HofK |
Nun ist die allgemeine Triangulation an der Reihe.
Dazu sind einige weitere Abläufe einzubinden. Bei der Kugel ist die Tangentialebene immer durch den Punkt selbst bestimmt. Er ist gleichzeitig die Normale. Im allgemeinen Fall benötigt man die implizite Funktion und ihre partiellen Ableitungen um den Gradienten bzw. die Normale und damit die Tangentialebene zu bestimmen.
Beispiel:
// heart https://www.math.hu-berlin.de/~filler/3D/flaechen.html
const qu = (x,y,z) => ( 2*x*x +y*y + z*z -1 );
const isf = ( x, y, z ) => ( qu(x,y,z)*qu(x,y,z)*qu(x,y,z) - 0.1*x*x*z*z*z - y*y*z*z*z );// IMPLICIT SURFACE Function
const dx = ( x, y, z ) => ( 3*qu(x,y,z)*qu(x,y,z)*4*x - 0.2*x*z*z*z );// PARTIAL DERIVATE to x
const dy = ( x, y, z ) => ( 3*qu(x,y,z)*qu(x,y,z)*2*y - 2*y*z*z*z );// PARTIAL DERIVATE to y
const dz = ( x, y, z ) => ( 3*qu(x,y,z)*qu(x,y,z)*2*z - 0.3*x*z*z*z - 3*y*y*z*z );// PARTIAL DERIVATE to z
const xs = 1;// x START POINT
const ys = 1;// y START POINT
const zs = 1;// z START POINT
Das kommt bei mir dann heraus:

Das Pascal Programm [...]  musste ich noch etwas näher inspizieren, um die zusätzlichen Dinge und ihre Feinheiten umzusetzen. Die Beschreibung des Algorithmus erfasst ja nicht das letzte, programmtechnisch aber eventuell relevante Detail. musste ich noch etwas näher inspizieren, um die zusätzlichen Dinge und ihre Feinheiten umzusetzen. Die Beschreibung des Algorithmus erfasst ja nicht das letzte, programmtechnisch aber eventuell relevante Detail.
Da habe ich nach vielen Jahren meine Kenntnisse in Pascal aufgefrischt.
Einige Dinge habe ich in Javascript aber anders gelöst. So gibt es kein Anfangssechseck, dafür ein Anfangsdreieck.
Auch die Berechnung der Winkel und Tangenten erfolgt anders.
Es sind noch Feinarbeiten und Tests nötig und für kompliziertere Flächen fehlen noch einige kleine Dinge in der Umsetzung des Algoritmus.
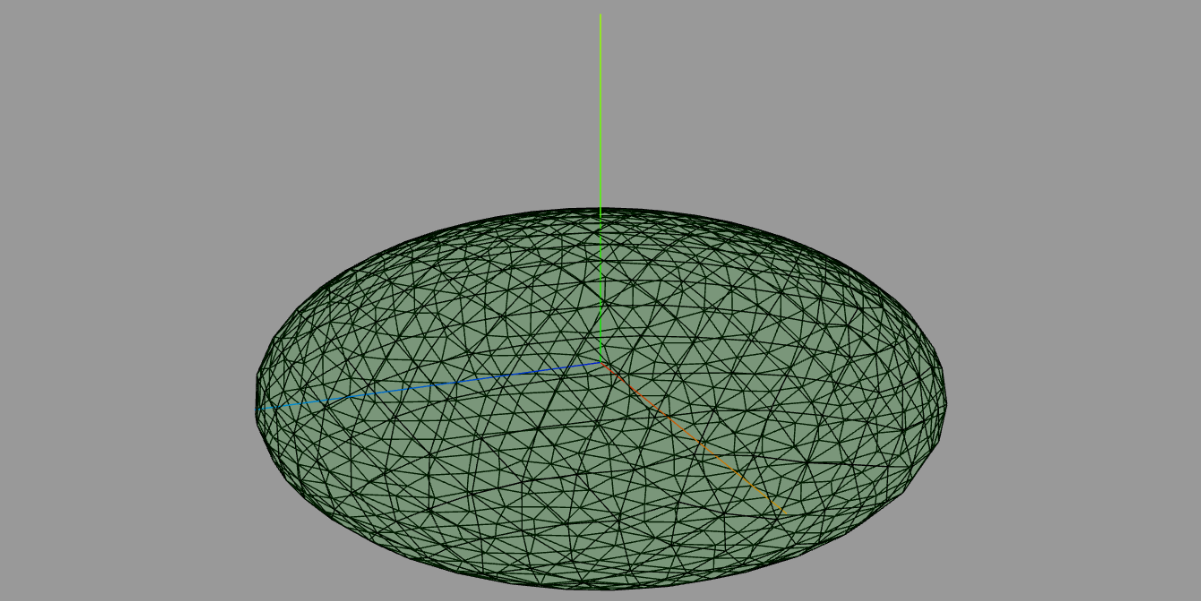
Eine gequetschte Kugel;
const isf = ( x, y, z ) => ( x * x + y * y / 3 + z * z - 1 );// IMPLICIT SURFACE Function
const dx = ( x, y, z ) => ( 2 * x );// PARTIAL DERIVATE to x
const dy = ( x, y, z ) => ( 2 / 3 * y );// PARTIAL DERIVATE to y
const dz = ( x, y, z ) => ( 2 * z );// PARTIAL DERIVATE to z
const xs = 0.1;// x START POINT
const ys = 0.05;// y START POINT
const zs = 0.95;// z START POINT
Aufgehalten hat mich tagelang einer meiner "blöden" Fehler.  Beim Kopieren und abändern stand an einer Stelle statt x y z dann in versteckter Form x y y. Beim Kopieren und abändern stand an einer Stelle statt x y z dann in versteckter Form x y y.
Es gab sehr merkwürdige Ergebnisse. Dadurch habe ich aber z.B. die Newton Iteration "zerlegt" und noch etwas dazugelernt. Aber daran lag es halt nicht, die war wie andere Dinge korrekt.
Immer wieder Korrektur gelesen und überlesen. Man ist betriebsblind. Es bräuchte eine Korrektor, der vom Inhalt keine Ahnung hat. Der findet so etwas garantiert. |
| | | | | | |
| | 
HofK | Noch eine einfache aber interessante Form.
const isf = ( x, y, z ) => ( x * x + y * y * y * y * y * y + z * z - 1 );// IMPLICIT SURFACE Function
const dx = ( x, y, z ) => ( 2 * x );// PARTIAL DERIVATE to x
const dy = ( x, y, z ) => ( 6 * y * y * y * y * y );// PARTIAL DERIVATE to y
const dz = ( x, y, z ) => ( 2 * z );// PARTIAL DERIVATE to z
const xs = 0.1;// x START POINT
const ys = 0.05;// y START POINT
const zs = 0.95;// z START POINT
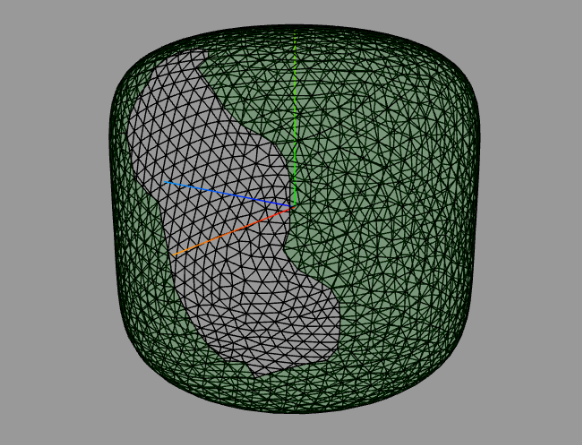
Darstellung bei unvollständigem Fortschritt der Triangulation. |
| | | | | | |
| | 
p.specht
 | Faszinierend!
(zit. Mr. Spok) |
| | | | XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 04.07.2019 ▲ |
| | |
|
AntwortenThemenoptionen | 391.622 Betrachtungen |
ThemeninformationenDieses Thema hat 10 Teilnehmer: |