| |
| |
|
| - Seite 1 - |
|

HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
|
| |
| |
| |
|
| |
| |
| - Seite 25 - |
|
|

HofK | HofK (22.07.2019)
Nach meiner Kenntnis gibt es keine Möglichkeit (oder keine hier praktikable) bei der Impliziten Funktion mit dem Newton Verfahren die Punkte "glatt " auf die Grenze zu bringen, wenn die Variable in der Funktion und ihren partiellen Ableitungen auftaucht.
Meine Kenntnis hat sich geändert.
Zwar bin ich im Netz weiterhin nicht fündig geworden, aber mir hat das Problem nach einer Pause keine Ruhe gelassen. Mit etwas Abstand und nochmal von der Basis ohne Begrenzung ausgehend, hat es nun geklappt. Dabei ist die Lösung gar nicht so weit von meinen Fehlversuchen entfernt. Den Grundgedanken hatte ich auch bei den ersten Versuchen - nur fehlerhaft umgesetzt. Wenn man sich erst einmal in einer Sackgasse verrannt hat, ist es aus.
Die Lösung besteht darin, nach der Bestimmung der neuen Punkte mit dem Newton-Verfahren zu prüfen, ob sie die Grenzen überschreiten. Wenn eine Koordinate die Grenze überschreitet, wird sie auf den Grenzwert zurückgesetzt. Dann wird die Newton-Iteration noch einmal ausgeführt. Dabei wird allerdings nicht der komplette Gradient (Vektor der partiellen Ableitungen) genutzt. Die Grenzkomponente wird auf 0 gesetzt. Damit wird die Newton-Iteration in der Grenzebene, also in zwei Koordinaten ausgeführt.
Abgesehen von Fällen wo das Verfahren nicht oder falsch konvergiert (Singularitäten), funktioniert es in den meisten Konstellationen. Nicht umsonst ist auch im originalen Basis-Algorithmus in Pascal eine Warnung im Code enthalten
writeln(cc,' WARNING tri (surface_point...): newton');
Drei Beispiele:
Kugel mit Kegel zweifach geschnitten

Sinus, dreifach geschnitten
const pi2 = Math.PI / 2;
const si = ( y ) => ( Math.sin( pi2 * y ) - 0.05 );
const isf = ( x, y, z ) => ( x * x + si( y ) * si( y ) + z * z - 1 );// IMPLICIT SURFACE Function
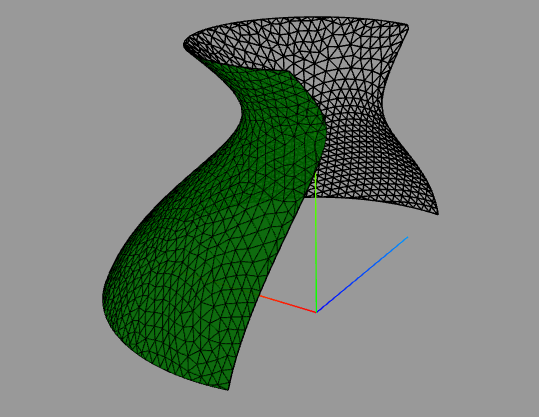
drei Zylinder, vierfach geschnitten

... und nun wieder Code optimieren und aufräumen. |
|
| |
| |
| |
|
|

p.specht
 | Höchste Zeit für den berühmten "Utah Teapot" [...]  ! ! |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 07.08.2019 ▲ |
|
| |
|
|

HofK | p.specht (07.08.2019)
Höchste Zeit für den berühmten "Utah Teapot" [...]  !
Zu spät!
Gibt es schon lange in three.js.
Seit Revision 56 (derzeit 107 aktuell ) dort zu finden.
Demo: [...] 
Geometrie: [...]  |
|
| |
| |
| |
|
|

p.specht
 | | Teapot klappt prima ... Bin überrascht, wie glatt er wirkt ! |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 09.08.2019 ▲ |
|
| |
|
|

HofK | Wieder eine Etappe geschafft.
Die Version mit Begrenzung ist fertiggestellt und in das THREEi Addon integriert.
Für unendliche Flächen wie Zylinder (siehe oben), aber auch zum Schnitt von anderen Flächen.
genus2 cut

Siehe
GitHub: [...] 
discourse: [...]  |
|
| |
| |
| |
|
|

HofK | Eine kleine Ergänzung.
Die Berechnung der Dreiecke der impliziten Flächen erfordert einen gewissen Aufwand. Daher kann es sinnvoll sein, das Ergebnis der Berechnung als komplette three.js BufferGeometry Definition zu exportieren.
Ich habe das auf GitHub hinzugefügt.
Die Datei triangulationImplicitSurfaceExportGeo.html erfüllt den Zweck. Siehe Ordner examples. Wenn man auf den Button Export Def drückt, wird der JavaScript Code angezeigt und in die Zwischenablage kopiert. Die ...32 Arrays werden auf die tatsächliche Länge gekürzt. Diese three.js BufferGeometry-Definition kann in die Datei implicitSurfaceImport.html an der markierten Stelle eingefügt werden. Die Definition kann auch einfach in eigene Projekte kopiert werden. |
|
| |
| |
| |
|
|

p.specht
 | Die Figur könnte ein Ausschnitt aus einer "Klein´schen Flasche" sein. Dass das nicht so ist, wird vermutlich erst bei Bewegung klar ...
Frage zum Teapot: Dreht sich die Lichtquelle eigentlich immer mit der Szene mit, oder kann man auch "Beleuchtung konstant von schräg vorne" definieren? |
|
| |
| Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 15.08.2019 ▲ |
|
| |
|
|

HofK | Die Kleinsche Flasche wird als parametrische BufferGeometry realisiert: [...] 
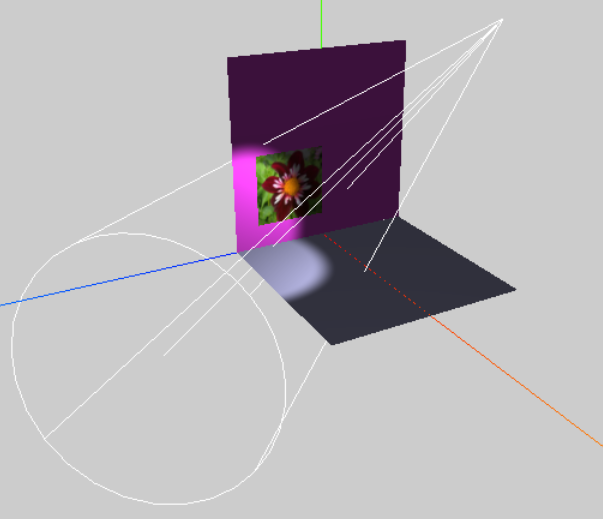
Es gibt im Framework three.js verschiedenartige Lichtquellen. Diese kann man kombinieren und nach Bedarf im 3D Raum positionieren. Sie sind im Zusammenspiel mit dem verwendeten Material zu verstehen. Ein dargestellter Körper (Mesh) beteht aus Geometrie und Material.
Dort [...]  ist ein Spot teilweise auf ein Bild gerichtet und es werden Hilfslinien angezeigt. ist ein Spot teilweise auf ein Bild gerichtet und es werden Hilfslinien angezeigt.
 |
|
| |
| |
| |
|
|

p.specht
 | |
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 15.08.2019 ▲ |
|
| |
|
|

HofK | HofK (30.07.2019)
Die Grafiken in den vorherigen Beiträgen wurden mit dem Lineal von IF [...]  aufgenommen. Sehr praktikabel. Funktioniert nicht mehr. Nun übe ich mit Firefox "Bildschirmfoto".
Firefox hilft aber nicht außerhalb des Browsers. Da habe ich nun Monosnap [...]  für mich entdeckt. Einige Tasten muss man umdefinieren, sie sind auf das englische Tastaturlayout ausgerichtet und haben mir in anderer Software Probleme gemacht. Mein Laptop hat zwischen Alt Gr und rechter Strg Taste eine bisher nie genutzte Taste. Sieht aus wie ein Menü oder ein Blatt mit drei Zeilen - keine Ahnung wozu sie dienen soll. Da drücke ich nun drauf und es funktioniert fast wie bei IF. Aber einige kleine Details hat IF noch besser gelöst! für mich entdeckt. Einige Tasten muss man umdefinieren, sie sind auf das englische Tastaturlayout ausgerichtet und haben mir in anderer Software Probleme gemacht. Mein Laptop hat zwischen Alt Gr und rechter Strg Taste eine bisher nie genutzte Taste. Sieht aus wie ein Menü oder ein Blatt mit drei Zeilen - keine Ahnung wozu sie dienen soll. Da drücke ich nun drauf und es funktioniert fast wie bei IF. Aber einige kleine Details hat IF noch besser gelöst! |
|
| |
| |
| |
|
|

p.specht
 | | Ich verwende Irfanview, für vieles gut, auch für selektive Screenshots! |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 21.08.2019 ▲ |
|
| |
|
|

HofK | Irfanview ist schon eine richtige Software-Suite, während Monosnap ein schlankes Tool ist. Startet bei mir mit dem System und lauert Resourcen schonend bis ich die "Spezialtaste" drücke.
Habe zwei mal gedrückt:
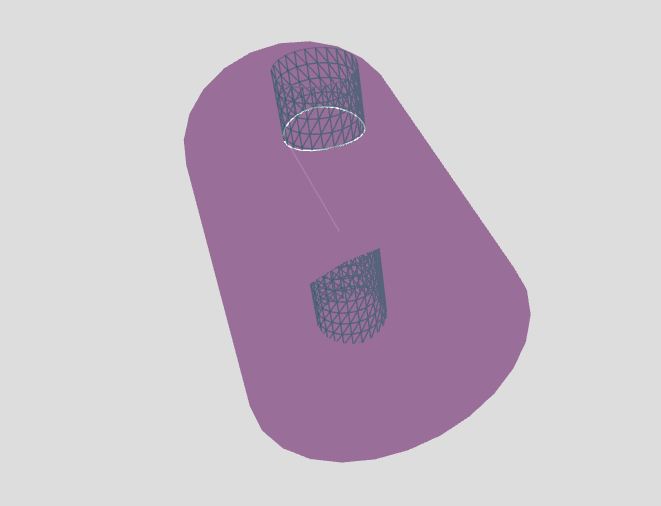

Als Vorbereitung für Zylinder und Torus mit kreisförmigen (deformierten) Löchern habe ich die Schnittlinien erzeugt. Für den Zylinder findet man die Herleitung dort: [...] 
Für den Torus habe ich nichts gefunden und selbst hergeleitet. Die vierfache Lösungsformel (biquadratisch) ist etwas komplizierter. |
|
| |
| |
| |
|