(953)  Anmelden

Deutsch
PHP, HTML & JavaScript- Forum

3D Grafik - WebGL mit three.js

 
- Seite 1 -



HofK
Auf einen heißen Tipp von IF hin, habe ich mir mal
three.js  [...]  angeschaut. Da  [...]  (ganz unten) die ersten Resultate.
 
31.01.2016  ▲
Vollständiges Zitat
Absatzweise zitierenZeilenweise zitieren
 



 
- Seite 27 -



p.specht

Könnte man einzelne Triangulations-Dreiecke farblich ändern? (Ein Narr kann mehr fragen als 10 Weise beantworten...)
 
XProfan 11
Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'...
23.09.2019  ▲
 




HofK
Auch das habe ich bisher nicht implementiert, ist aber leicht möglich. Im Addon ist es realisiert. [...] 



In der Sandbox kann man es probieren.  [...] 

 
23.09.2019  ▲
 




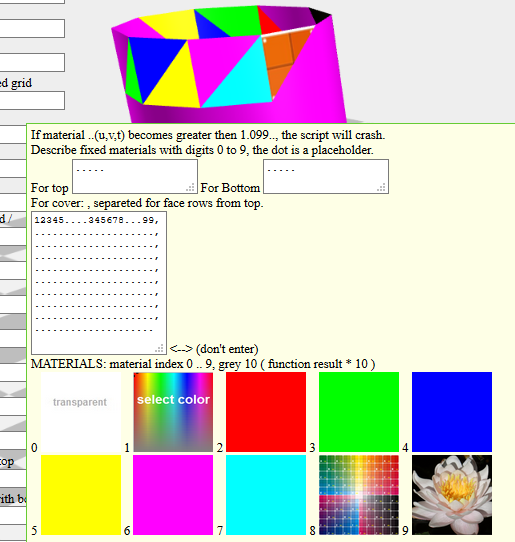p.specht

Supi!
 
XProfan 11
Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'...
23.09.2019  ▲
 




HofK
Der Zylinder mit Löchern und Randanpassung ist fertig. Dank des sehr flexiblen Algorithmus von Prof. E. Hartmann (siehe weiter oben) ist es möglich, fast beliebige Begrenzungen als Front zu definieren und so Formen nach Wunsch zu erzeugen.

Dort ausprobieren  [...] 

Auf GitHub eine Variante im Addon THREEi  [...] 

Auf discourse  [...] 

Man kann die Zylinder zu einer Innengeometrie zusammenfügen.



Dort ausprobieren, den Schieber benutzen! [...] 

Wenn man d (ungefähre Seitenlänge der Dreiecke) einheitlich wählt, passen die Kanten perfeckt.

 
25.09.2019  ▲
 




HofK
HofK (25.09.2019)
Wenn man d (ungefähre Seitenlänge der Dreiecke) einheitlich wählt, passen die Kanten perfeckt.


Um das auch im Zusammenspiel mit Kugeln zu ermöglichen, habe ich eine weitere Variante der Kugel mit Löchern erstellt. Sie entspricht im grundsätzlichen Aufbau dem Algorithmus für den Zylinder.

Die vorherige Kugelvariante hat den festen Radius 1 und muss mit three.js Methode .scale auf den gewünschten Radius gebracht werden. Dafür ist dort der Aufwand geringer und es wird auch eine andere Art der Winkelberechnung benutzt. 

Im Addon THREEi werden die Varianten automatisch anhand der Parameter unterschieden.

Siehe GitHub:  [...]  [...]  , discourse:  [...] 

Dort ausprobieren:  [...] 
 
08.10.2019  ▲
 




p.specht

Einfach toll! Ist das eine Sichtbarkeits-Ebene, die man da verschiebt, oder die Anzahl der gezeichneten Dreiecke?
 
XProfan 11
Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'...
08.10.2019  ▲
 




HofK
Die 3D Darstellung erfolgt aus internen Gründen ( JavaScript, WebGL, three.js) erst nach vollständiger Berechnung. Außerdem ist das so flott, das man wenig sehen würde, ließe es sich bei der Berechnung darstellen. Der Trick mit dem Schieber ist ein einfaches three.js Feature. In der Animationsschleife kann man die Anzahl der zu zeichnenden Dreiecke variieren.

g.setDrawRange( 0, range.value * 3 * progressFactor );





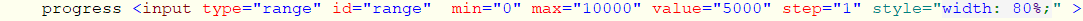
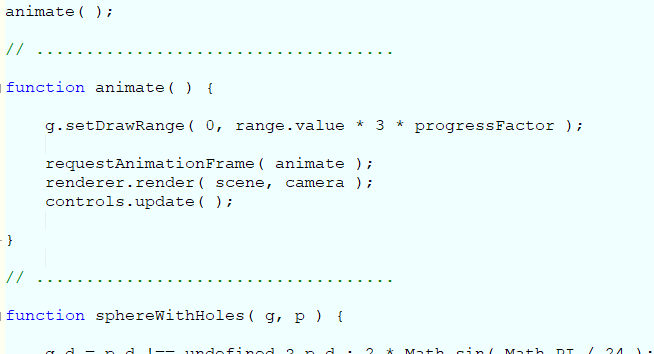
Jeder Punkt hat 3 Koordinaten, den Faktor kann man festlegen:
let progressFactor = 1.1;
 
09.10.2019  ▲
 




HofK
HofK (22.08.2019)
Als Vorbereitung für Zylinder und Torus mit kreisförmigen (deformierten) Löchern habe ich die Schnittlinien erzeugt. Für den Zylinder findet man die Herleitung dort:  [...] 

Für den Torus habe ich nichts gefunden und selbst hergeleitet. Die vierfache Lösungsformel (biquadratisch) ist etwas komplizierter.


Das war für senkrecht mittig durch den Torus gehende Zylinder. Für waagerecht mittig schneidende Zylinder ist die Rechnung ähnlich möglich. Durch Drehung um die z Achse (aus der Bildebene heraus) kann man dann weitere Löcher erzeugen.



Beim Versuch ein allgemein liegendes Loch zu erzeugen, erhalte ich eine allgemeine Gleichung 3. Grades. Die Lösung ist nicht so einfach möglich. Wer es braucht: [...] 

Interessanterweise ist zu diesem Problem die deutsche Seite am aussagekräftigsten. In Englisch und anderen Sprachen (Formeln sind recht international) wurde ich nicht so fündig. 


UPDATE: Es ist nich besser! Ich hatte mich verrechnet, es wird eine allgemeine Gleichung 4. Grades (Quartische Gleichung), nicht biquadratisch!  [...] 

Ich werde darauf verzichten, zumal es bei Bedarf eine weitere Lösungsmöglichkeit gibt.  [...]  Seite 94 ff.

8.2 Intersection surface – surface
8.2.1 IS of two implicit surfaces
Thealgorithm:The heart of the algorithm is procedurecurvepointwhich determines for a starting pointQ0:q0in the ”neighborhood” of the intersection curve a pointP:pon the intersection curve.
 
09.10.2019  ▲
 




p.specht

 
XProfan 11
Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'...
09.10.2019  ▲
 




HofK
UPDATE zu meinem letzten Beitrag wegen Schusselfehlers!
 
09.10.2019  ▲
 




p.specht

Die quartische Gleichung löst man am besten per Newton-Raphson-Näherung.

Ansonsten müßte man folgendes Monster kanonisieren, memoisieren und auf komplexe Zahlen erweitern:

x1=-(sqrt((3*(8*a^2*d-4*a*b*c+b^3))/(2*a^2*sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))-(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)-(12*a*e-3*b*d+c^2)/(9*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))-(2*a*c-b^2)/(2*a^2)-c/(3*a)))/(2)-(sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))/(12*a)-b/(4*a)

x2=(sqrt((3*(8*a^2*d-4*a*b*c+b^3))/(2*a^2*sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))-(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)-(12*a*e-3*b*d+c^2)/(9*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))-(2*a*c-b^2)/(2*a^2)-c/(3*a)))/(2)-(sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))/(12*a)-b/(4*a)

x3=-(sqrt(-(3*(8*a^2*d-4*a*b*c+b^3))/(2*a^2*sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))-(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)-(12*a*e-3*b*d+c^2)/(9*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))-(2*a*c-b^2)/(2*a^2)-c/(3*a)))/(2)+(sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))/(12*a)-b/(4*a)

x4=(sqrt(-(3*(8*a^2*d-4*a*b*c+b^3))/(2*a^2*sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))-(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)-(12*a*e-3*b*d+c^2)/(9*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))-(2*a*c-b^2)/(2*a^2)-c/(3*a)))/(2)+(sqrt((36*a^2*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(2/3)+(9*b^2-24*a*c)*(
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3)+48*a*e-12*b*d+4*c^2)/((
sqrt(-256*a^3*e^3-(-192*a^2*b*d-128*a^2*c^2+144*a*b^2*c-27*b^4)*e^2-((144*a^2*c-6*a*b^2)*d^2+(18*b^3*c-80*a*b*c^2)*d+16*a*c^4-4*b^2*c^3)*e+27*a^2*d^4-(18*a*b*c-4*b^3)*d^3-(b^2*c^2-4*a*c^3)*d^2)/(2*3^(3/2)*a^3)
-(a*(72*c*e-27*d^2)-27*b^2*e+9*b*c*d-2*c^3)/(54*a^3))^(1/3))))/(12*a)-b/(4*a)]

Das lassen wir aber hübsch bleiben.
Gruss
 
Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'...
10.10.2019  ▲
 




HofK
p.specht (10.10.2019)
Das lassen wir aber hübsch bleiben.



Sicher ist das eine interessante Formel, aber unheimlich aufwändig und bei meiner Schusseligkeit fehlt da dann bestimmt etwas. Das zu finden, wäre wie die Stecknadel im Heuhaufen finden. Dann doch lieber irgend eine algorithmische Lösung mit dem guten alten Newton.

Ich lasse das erst mal sacken und mache einfachere Dinge.

Kugel mit Zylinder, aber exzentrisch. Da ist die Rechnung fast primitiv!





fast fertig:
KompilierenMarkierenSeparieren
for ( let i = 0, alpha = 0; i < countH; i ++, alpha += 2 * Math.PI / countH ) {

    // cut line
    xa = exc - rHole * Math.cos( alpha );
    ya = Math.sqrt( g.radius * g.radius - rHole * rHole - exc * exc + 2 * rHole * exc * Math.cos( alpha ) );
    za = rHole * Math.sin( alpha );
    ...



Bei der Kugel lässt sich das an jede Position drehen. Ein Problem gibt es noch, wenn der in die Schnittlinie passende Zylinder über die Kugel hinausragt. Dann gibt es eine Vereinigung der beiden Schnittlinien der Durchgänge des Zylinders durch die Kugel.
 
10.10.2019  ▲
 



◄►

Antworten


Thementitel, max. 100 Zeichen.
 

Systemprofile:

Kein Systemprofil angelegt. [anlegen]

XProfan:

 Beitrag  Schrift  Smilies  ▼ 

Bitte anmelden um einen Beitrag zu verfassen.
 

Themenoptionen

Ungelesen
Abonnieren
Merkliste
Hinweise
Gäste
Löschen
Ständig
Erledigt

333.020 Betrachtungen

Unbenanntvor 0 min.
HofK vor 24 Tagen
Rschnett24.08.2024
Michael W.28.03.2024
Thomas Zielinski17.02.2024
Mehr...

Themeninformationen

Dieses Thema hat 10 Teilnehmer:

HofK (426x)
p.specht (100x)
iF (10x)
Michael W. (5x)
ByteAttack (4x)
RudiB. (3x)
Jörg Sellmeyer (1x)
RGH (1x)
Georg Teles (1x)
E.T. (1x)


Admins  |  AGB  |  Anwendungen  |  Autoren  |  Chat  |  Datenschutz  |  Download  |  Eingangshalle  |  Hilfe  |  Händlerportal  |  Impressum  |  Mart  |  Schnittstellen  |  SDK  |  Services  |  Spiele  |  Suche  |  Support

Ein Projekt aller XProfaner, die es gibt!


Mein XProfan
Private Nachrichten
Eigenes Ablageforum
Themen-Merkliste
Eigene Beiträge
Eigene Themen
Zwischenablage
Abmelden
 Deutsch English Français Español Italia
Übersetzungen

Datenschutz


Wir verwenden Cookies nur als Session-Cookies wegen der technischen Notwendigkeit und bei uns gibt es keine Cookies von Drittanbietern.

Wenn du hier auf unsere Webseite klickst oder navigierst, stimmst du unserer Erfassung von Informationen in unseren Cookies auf XProfan.Net zu.

Weitere Informationen zu unseren Cookies und dazu, wie du die Kontrolle darüber behältst, findest du in unserer nachfolgenden Datenschutzerklärung.

einverstandenDatenschutzerklärung
Ich möchte keinen Cookie