| |
| |
|
| - Seite 1 - |
|

HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
|
| |
| |
| |
|
| |
| |
| - Seite 21 - |
|
|

HofK | Diese Lösung ist recht einfach, erzeugt aber keine kreisförmigen Öffnungen. Man kann sie aber eventuell als Ausgangspunkt nehmen und das Netz passend "verbiegen". Ich werde es probieren.
 |
|
| |
| |
| |
|
|

HofK | Beim herumexperimentieren gibt es immer wieder interessant aussehende Fehlentwürfe.
Da sind wohl Vorzeichen nicht ganz in Ordnung und die Radiuskonstante wurde an einer Stelle vergessen. Sieht aber interessant aus.
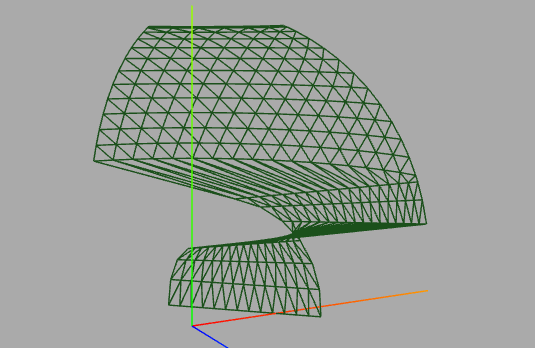
Fehler gefunden, nun sieht es so aus.

Man erkennt schon, wie es werden soll. Das Problem ist, dass die sonst horizontalen Bögen hier schräg verlaufen müssen und sich unterschiedliche face-Reihen ergeben.
Betrachtet man die Konstruktion aus einer anderen Perspektive, sieht man besser, dass ich noch geschummelt habe.

Um das Verfahren zu testen, habe ich die linke und rechte Kante der unteren Bereiche einfach durch Geraden verbunden.
Daraus müssen nun noch "Geraden auf der Kugel" - also Kreisbögen werden.
Da kann ich wieder die Radiuskonstante vergessen!
Die Rechnerei für dieses Verfahren ist komplizierter als im ersten Entwurf, erscheint mir aber insgesamt effizienter. Allerdings hat man durch die "schrägen" Linien/Bögen keine so schöne Symmetrie- |
|
| |
| |
| |
|
|

p.specht
 | Könnte es sein, daß Du ein Faible für Netzstrümpfe hast 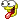 ? ? |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 14.04.2019 ▲ |
|
| |
|
|

HofK | Eher ein Faible für mathematische Netze, Netzstrümpfe sind mathematisch sehr schwer zu erfassen. Da nimmt man dann eine Modellierungs-Software.
Das Netz aus Dreiecken ist die Grundlage der 3D Grafik, also führt nichts daran vorbei.
Und es gibt so schöne Fehlentwürfe!
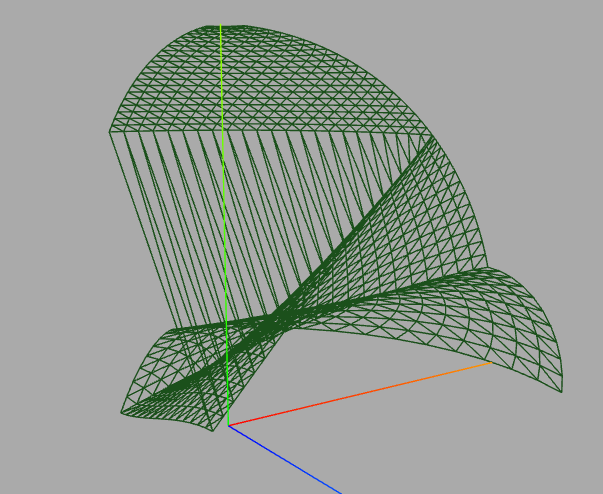

Aber wie das Sprichwort sagt "Ende gut, alles gut"

Die Lösung erfordert weniger Teilflächen als der erste Ansatz, ist aber nicht so symmetrisch, wenn man verschieden große Öffnungen hat (hier alle gleich ). Allerdings ist die Rechnung etwas "spezifisch", aber gut überschaubar.
Der Code muss noch optimiert werden, momentan noch "wirr" und nicht vorzeigbar. |
|
| |
| |
| |
|
|

HofK | Die Kugel mit unterschiedlich großen Öffnungen, der Code ist noch in Überarbeitung.
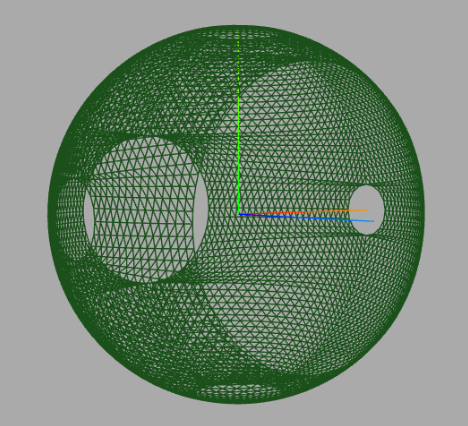
Mich hat dann doch der Vergleich der Varianten interessiert. Die symmetrische Lösung macht bei der Erweiterung von einem auf acht Oktanten recht viel Aufwand und es hakt noch.
Aber wieder ein schöner Fehlentwurf. Statt wie nötig von hinten nach vorn die Indizes im Zentrum andersherum bearbeitet.

So soll es sein.

Es gibt dann insgesamt 8 mal 7 = 56 Teilflächen! |
|
| |
| |
| |
|
|

HofK | Da sind die 56 Teilflächen:

Alle Öffnungen sind verschieden groß-
Nimmt man überall die maximale Öffnung, sind tatsächlich nur 32 Teilflächen zu erzeugen. Die maximale Öffnung ist bei dieser Variante auf den halben Äquator begrenzt. Bei der anderen Variante kann eine Öffnung maximal sogar bis zum Äquator gehen (Halbkugel). Allerdings dürfen sich benachbarte Öffnungen dort nicht überschneiden.
Füllt man die Öffnungen mit THREE.CircleBufferGeometry erhält man einen sehr speziellen Spielwürfel.
Aber dazu muss ich erst noch die uv-Werte berechnen. |
|
| |
| |
| |
|
|

HofK | Die Berechnung der uv-Werte konnte ich nach kleinen Anpassungen des Codes dieser symmetrischen Kugelvariante von der anderen Variante übernehmen. Diese Berechnung hatte ich vorher dort schon getestet.
Es ist wie gewohnt eine kleine Rechnerei mit trigonometrischen Funktionen.


Nun muss der Code noch ein wenig aufgeräumt und in die Form für mein Addon THREEg gebracht werden. |
|
| |
| |
| |
|
|

p.specht
 | | Würde eine Globus-Karte unverzerrt dargestellt? Oder wie müsste deren Textur aussehen? |
|
| |
| Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 23.04.2019 ▲ |
|
| |
|
|

HofK | Da ich die Kugel in acht einzelne Teile zerlege um jede Teilfläche mit einer anderen Textur versehen zu können (Multimaterial) ist eine Globuskarte hier nicht sinnvoll möglich.
Dazu benutzt man die einfache Kugeldefinition von THREE.js mit Längen - und Breitengraden.
Man kann eine Globuskarte natürlich auf alle möglichen Formen aufbringen. Siehe mein Beispielbild rechts oben auf sandbox .threejs.hofk [...] 
Mir geht es hier um die 6 möglichen gleichzeitigen Öffnungen in der Kugel . |
|
| |
| |
| |
|
|

HofK | Geschafft!
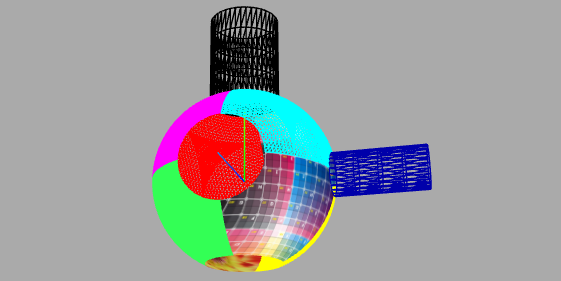

Die beiden Varianten: [...]  [...] [...] 
Die berechneten Eigenschaften
g.cutRadius = [];// calculated radius of cut circles px, nx, py, ny, pz, nz - for external use
g.cutDistance = [];// calculated distance of the cut circles to the center px, nx, py, ny, pz, nz - for external use
g.cutSegments = [];// segments of the cut circles - for external use
ermöglichen die Andockung von Zylindern. Damit kann man ein Labyrinth mit runden Formen erzeugen.
Ich werde die Kugeln in das Addon aufnehmen. |
|
| |
| |
| |
|
|

p.specht
 | Könnte man damit das Atomium [...]  in Brüssel nachbauen? in Brüssel nachbauen? |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 27.04.2019 ▲ |
|
| |
|
|

HofK | Nein, da beim Atomium die Verbindungen nicht entsprechend zu den Koordinatenebenen liegen.
Allerdings benötigt man für eine reine Außenansicht meine spezielle Konstruktion nicht. Man kann die three.js Kugel beliebig mit dem three.js Zylinder kombinieren.
Die Öffnungen benötigt man nur für innere Ansichten. Da ist das Atomium sicher komplexer und man nimmt ein Tool wie Blender. Garantiert viel Arbeit. Mag sein, das gibt es schon?
_______________________________________________________________
Ich habe die Konstruktion so erweitert, dass nur gewünschte Teile der Kugel erzeugt werden.
function createSphereCutSymmetric( g, radius, fineness, cut, parts ) {
// BufferGeometry, radius, fineness (1/4 equator),
// cut[ px, nx, py, ny, pz, nz ] max. 2*fineness
// parts [ 1, 1, 1, 1, 1, 0, 0, 1 ] 1 for create part, otherwise arbitrary

createSphereCut( g, 2, 40, [ 6, 3, 10, 11, 12, 0 ], [ 1, 1, 1, 1, 1, 0, 0, 1 ] );
// BufferGeometry, radius, equator,
// cut[ px, nx, py, ny, pz, nz ] max. equator, non-overlapping,
// parts [ 1, 1, 1, 1, 1, 0, 0, 1 ] 1 for create part, otherwise arbitrary

Bei discourse.threejs.hofk. de [...]  bereits integriert. bereits integriert. |
|
| |
| |
| |
|