PHP, HTML & JavaScript- Forum | | | | | | - Seite 1 - |
| 
HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
| | | | | | |
| | | | | | - Seite 22 - |
| | 
HofK | Die Kugel mit den Schnitten nun im Addon THREEg auf GitHub. [...] 
Die beiden Varianten habe ich durch einen Parameter
realisiert.
const g = new THREE.BufferGeometry( );
g.createSphereCut = THREEg.createSphereCut;
g.createSphereCut( {
radius: 2,
equator: 38,// is set to divisible by 4 (= 40) if symmetric: true
cut: [ 6, 3, 10, 11, 12, 0 ],// if symmetric max. 1/2 equator, otherwise equator, non-overlapping
parts: [ 1, 1, 1, 1, 1, 0, 0, 1 ],// 1 for create part, otherwise arbitrary
//symmetric: true // default is false
} );
const mesh = new THREE.Mesh( g, material );// multimaterial array with 8 materials
scene.add( mesh );
|
| | | | | | |
| | 
HofK | Bei der Sichtung meiner Kugeldesigns ist mir aufgefallen, dass ich keine elementare Version für non-indexed BufferGeometry habe. Die im Addon benutzte Variante ist mit vielen Funktionen überladen und so ist das Grundprinzip kaum mehr erkennbar.
Deshalb habe ich eine Version erstellt, die mit minimalem Rechenaufwand auskommt und sofort das Float32Array der Positionen der unabhängigen Dreiecke ("Dreieckssuppe") füllt.
Dadurch ist die Hilfsfunktion zur Anzeige der Dreiecksnummern länger als die Funktion zur Erzeugung der Geometrie!

Dort zu betrachten: [...]  bzw. unmittelbar [...] bzw. unmittelbar [...] 
Der komplette Code:
<!DOCTYPE html>
<head>
<title> SphereNonIndexed </title>
<meta charset="utf-8" />
<style>
body {
margin: 0;
}
</style>
</head>
<body> </body>
<script src="../js/three.min.104.js"></script>
<script src="../js/OrbitControls.js"></script>
<script>
// @author hofk
'use strict';
const scene = new THREE.Scene();
const camera = new THREE.PerspectiveCamera( 55, window.innerWidth / window.innerHeight, 0.01, 1000 );
camera.position.set( 1, -1, 6 );
const renderer = new THREE.WebGLRenderer( { antialias: true } );
renderer.setSize( window.innerWidth, window.innerHeight );
renderer.setClearColor( 0xaaaaaa, 1 );
const container = document.createElement('div' );
document.body.appendChild( container );
container.appendChild( renderer.domElement );
const controls = new THREE.OrbitControls( camera, renderer.domElement );
const axesHelper = new THREE.AxesHelper( 2 );
scene.add( axesHelper );
var material1 = new THREE.MeshBasicMaterial( { color: 0x559955, transparent: true, opacity: 0.3, side: THREE.FrontSide, wireframe: false } );
var material2 = new THREE.MeshBasicMaterial( { color: 0x000000, wireframe: true} );
const g = new THREE.BufferGeometry( );
createSphere( g, 2, 10 );
// BufferGeometry, radius, equator,
const mesh1 = new THREE.Mesh( g, material1 );
scene.add( mesh1 );
const mesh2 = new THREE.Mesh( g, material2 );
scene.add( mesh2 );
let numbersHelper = new vertexFaceNumbersHelper( mesh2, 2, 0.04, 0x0000aa );// only mode 2, no vertices defined
numbersHelper.update( 2 );
animate();
function animate() {
requestAnimationFrame( animate );
renderer.render( scene, camera );
controls.update();
}
function createSphere( g, radius, equator ) {
let eqt = equator;
const sumON = ( n ) => ( n * n );// Sum odd numbers
const pi2 = Math.PI / 2;
let positionCount, posIdx, aIdx, bIdx, cx, cy, cz, theta, phi;
positionCount = sumON( eqt ) * 6 * 9;// hemisphere
g.positions = new Float32Array( positionCount );
g.addAttribute('position', new THREE.BufferAttribute( g.positions, 3 ) );
// previus ring
let x0 = [];
let y0 = [];
let z0 = [];
let x = [];
let y = [];
let z = [];
theta = pi2 / eqt;
x.push( radius * Math.sin( theta ) );
y.push( radius * Math.cos( theta ) );
z.push( 0 );
posIdx = 0;
for ( let p = 0; p < 6; p ++ ) {// pole faces, 6 parts
phi = 2 * Math.PI * ( p + 1 ) / 6;// start next part
g.positions[ posIdx ] = 0;// pole
g.positions[ posIdx + 1 ] = radius;
g.positions[ posIdx + 2 ] = 0;
g.positions[ posIdx + 3 ] = x[ p ];
g.positions[ posIdx + 4 ] = y[ p ];
g.positions[ posIdx + 5 ] = z[ p ];
cx = radius * Math.sin( theta ) * Math.cos( phi );
cy = radius * Math.cos( theta );
cz = -radius * Math.sin( theta ) * Math.sin( phi );
x.push( cx );
y.push( cy );
z.push( cz );
g.positions[ posIdx + 6 ] = cx;
g.positions[ posIdx + 7 ] = cy;
g.positions[ posIdx + 8 ] = cz;
posIdx += 9;
}
for ( let i = 1; i < eqt; i ++ ) {
x0 = [];
y0 = [];
z0 = [];
x0 = x.slice( );
y0 = y.slice( );
z0 = z.slice( );
x = [];
y = [];
z = [];
theta = pi2 * ( i + 1 ) / eqt;// refers to next ring
for ( let p = 0; p < 6; p ++ ) {// 6 parts
for ( let j = 0; j < i; j ++ ) {
if ( p === 0 && j === 0 ) {// initial per ring
x.push( radius * Math.sin( theta ) );
y.push( radius * Math.cos( theta ) );
z.push( 0 );
}
aIdx = p * i + j;
bIdx = p * ( i + 1 ) + j;
// left face
g.positions[ posIdx ] = x0[ aIdx ];// a
g.positions[ posIdx + 1 ] = y0[ aIdx ];
g.positions[ posIdx + 2 ] = z0[ aIdx ];
g.positions[ posIdx + 3 ] = x[ bIdx ];// b
g.positions[ posIdx + 4 ] = y[ bIdx ];
g.positions[ posIdx + 5 ] = z[ bIdx ];
phi = 2 * Math.PI / 6 * ( p + ( j + 1 ) / ( i + 1) );
cx = radius * Math.sin( theta ) * Math.cos( phi );
cy = radius * Math.cos( theta );
cz = -radius * Math.sin( theta ) * Math.sin( phi );
x.push( cx );
y.push( cy );
z.push( cz );
g.positions[ posIdx + 6 ] = cx;// c
g.positions[ posIdx + 7 ] = cy;
g.positions[ posIdx + 8 ] = cz;
posIdx += 9;
// right face
g.positions[ posIdx ] = x0[ aIdx ];// a
g.positions[ posIdx + 1 ] = y0[ aIdx ];
g.positions[ posIdx + 2 ] = z0[ aIdx ];
g.positions[ posIdx + 3 ] = cx;// c
g.positions[ posIdx + 4 ] = cy;
g.positions[ posIdx + 5 ] = cz;
g.positions[ posIdx + 6 ] = x0[ aIdx + 1 ];// a1
g.positions[ posIdx + 7 ] = y0[ aIdx + 1 ];
g.positions[ posIdx + 8 ] = z0[ aIdx + 1 ];
posIdx += 9;
}
// last face, like a left face
aIdx = p * i + i;
g.positions[ posIdx ] = x0[ aIdx ];// a, like j equals i
g.positions[ posIdx + 1 ] = y0[ aIdx ];
g.positions[ posIdx + 2 ] = z0[ aIdx ];
g.positions[ posIdx + 3 ] = cx;// equals last c
g.positions[ posIdx + 4 ] = cy;
g.positions[ posIdx + 5 ] = cz;
phi = 2 * Math.PI / 6 * ( p + 1 );// equals start next part
cx = radius * Math.sin( theta ) * Math.cos( phi );
cy = radius * Math.cos( theta );
cz = -radius * Math.sin( theta ) * Math.sin( phi );
x.push( cx );
y.push( cy );
z.push( cz );
g.positions[ posIdx + 6 ] = cx;
g.positions[ posIdx + 7 ] = cy;
g.positions[ posIdx + 8 ] = cz;
posIdx += 9;
}
}
}
function vertexFaceNumbersHelper( mesh, mode, size, color ) {
// mode: 0 nothing, 1 vertex, 2 face, 3 vertex & face
// for non indexed BufferGeometry
var verticesCount;
var facesCount;
var vertexNumbers = [];
var faceNumbers = [];
var materialDigits = new THREE.LineBasicMaterial( { color: color } );
var geometryDigit = [];
var digit = [];
var d100, d10, d1;// digits
var coordDigit = [];// design of the digits
var digitPositions = [];
function numbering() {
i1 ++;// starts with -1 + 1 = 0
if ( i1 === 10 ) {i1 = 0; i10 ++ }
if ( i10 === 10 ) {i10 = 0; i100 ++ }
if ( i100 === 10 ) {i100 = 0 }// hundreds (reset when overflow)
if ( i100 > 0 ) {
d100 = digit[ i100 ].clone();// digit for hundreds
board.add( d100 );// on the board ...
d100.position.x = -8 * 0.1 * size;// ... move slightly to the left
}
if ( ( i100 > 0 ) || ( ( i100 === 0 ) && ( i10 > 0 ) ) ) {// no preceding zeros tens
d10 = digit[ i10 ].clone();// digit for tenth
board.add( d10 );// on the board
}
d1 = digit[ i1 ].clone();// digit
board.add( d1 );// on the board ...
d1.position.x = 8 * 0.1 * size;// ... move slightly to the right
}
coordDigit[ 0 ] = [ 0,0, 0,9, 6,9, 6,0, 0,0 ];
coordDigit[ 1 ] = [ 0,6, 3,9, 3,0 ];
coordDigit[ 2 ] = [ 0,9, 6,9, 6,6, 0,0, 6,0 ];
coordDigit[ 3 ] = [ 0,9, 6,9, 6,5, 3,5, 6,5, 6,0, 0,0 ];
coordDigit[ 4 ] = [ 0,9, 0,5, 6,5, 3,5, 3,6, 3,0 ];
coordDigit[ 5 ] = [ 6,9, 0,9, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 6 ] = [ 6,9, 0,9, 0,0, 6,0, 6,5, 0,5 ];
coordDigit[ 7 ] = [ 0,9, 6,9, 6,6, 0,0 ];
coordDigit[ 8 ] = [ 0,0, 0,9, 6,9, 6,5, 0,5, 6,5, 6,0, 0,0 ];
coordDigit[ 9 ] = [ 6,5, 0,5, 0,9, 6,9, 6,0, 0,0 ];
if ( mode === 1 || mode === 3 ) {
verticesCount = mesh.geometry.vertexPositions.length;
}
if ( mode === 2 || mode === 3 ) {
facesCount = mesh.geometry.positions.length / 9;
}
for ( var i = 0; i < 10; i ++ ) {
geometryDigit[ i ] = new THREE.BufferGeometry();
digitPositions[ i ] = new Float32Array( coordDigit[ i ].length / 2 * 3 );
geometryDigit[ i ].addAttribute('position', new THREE.BufferAttribute( digitPositions[ i ], 3 ) );
for ( var j = 0; j < coordDigit[ i ].length/ 2; j ++ ) {
digitPositions[ i ][ j * 3 ] = 0.1 * size * coordDigit[ i ][ 2 * j ];
digitPositions[ i ][ j * 3 + 1 ] = 0.1 * size * coordDigit[ i ][ 2 * j + 1 ];
digitPositions[ i ][ j * 3 + 2 ] = 0;
}
digit[ i ] = new THREE.Line( geometryDigit[ i ], materialDigits );
}
if ( mode === 1 || mode === 3 ) {
var i100 = 0;
var i10 = 0;
var i1 = -1;
for ( var i = 0; i < verticesCount ; i ++ ) {
// Number on board, up to three digits are pinned there
var board = new THREE.Mesh( new THREE.BufferGeometry() );
numbering();// numbering the vertices, hundreds ...
vertexNumbers.push( board );// place the table in the vertex numbering data field
mesh.add( vertexNumbers[ i ] );
}
}
if ( mode === 2 || mode === 3 ) {
var i100 = 0;
var i10 = 0;
var i1 = -1;
for ( var i = 0; i < facesCount ; i ++ ) {
// Number on board, up to three digits are pinned there
var board = new THREE.Mesh( new THREE.BufferGeometry() );
numbering();// numbering the facesces, hundreds ...
faceNumbers.push( board );// place the table in the face numbering data field
mesh.add( faceNumbers[ i ] );
}
}
// update helper
this.update = function ( mode ) {
var x, y, z;
if ( mode === 1 || mode === 3 ) {
for( var n = 0; n < vertexNumbers.length; n ++ ) {
vertexNumbers[ n ].position.set( mesh.geometry.positions[ mesh.geometry.vertexPositions[ n ][ 0 ] ], mesh.geometry.positions[ mesh.geometry.vertexPositions[ n ][ 0 ] + 1 ], mesh.geometry.positions[ mesh.geometry.vertexPositions[ n ][ 0 ] + 2] );
vertexNumbers[ n ].quaternion.copy(camera.quaternion);
}
}
if ( mode === 2 || mode === 3 ) {
for( var n = 0; n < faceNumbers.length; n ++ ) {
x = 0;
x += mesh.geometry.positions[ 9 * n ];
x += mesh.geometry.positions[ 9 * n + 3 ];
x += mesh.geometry.positions[ 9 * n + 6 ];
x /= 3;
y = 0;
y += mesh.geometry.positions[ 9 * n + 1 ];
y += mesh.geometry.positions[ 9 * n + 4 ];
y += mesh.geometry.positions[ 9 * n + 7 ];
y /= 3;
z = 0;
z += mesh.geometry.positions[ 9 * n + 2 ];
z += mesh.geometry.positions[ 9 * n + 5 ];
z += mesh.geometry.positions[ 9 * n + 8 ];
z /= 3;
faceNumbers[ n ].position.set( x, y, z );
faceNumbers[ n ].quaternion.copy(camera.quaternion);
}
}
}
}
</script>
</html>
|
| | | | | | |
| | 
HofK | Der obige Code ergibt nur eine Halbkugel mit 6 Teilen.
Ich habe auf n Teile verallgemeinert und durch einfache Kopieroperationen mit Vertauschen die zweite Halbkugel generiert.
Man kann dabei unmittelbar mit dem für die Darstellung verantwortlichem Datenfeld g.positions
positionCount = sumON( eqt ) * parts * 2 * 9;
g.positions = new Float32Array( positionCount );
g.addAttribute( 'position', new THREE.BufferAttribute( g.positions, 3 ) );
arbeiten.
Das ermöglicht eine sehr kompakte Realisierung.
Die Vertauschung der Ecken b und c ergibt den richtigen Umlaufsinn. Ansonsten wären Vor- und Rückseite vertauscht. Arbeitet man nur mit Material mit THREE.DoubleSide oder mit wireframe: true, ist das unerheblich und man könnte diesen Schritt noch einsparen.
Dort zu finden: [...] 
Für den Nummernhelfer habe ich hier einfach mein Addon THREE.g eingebunden.
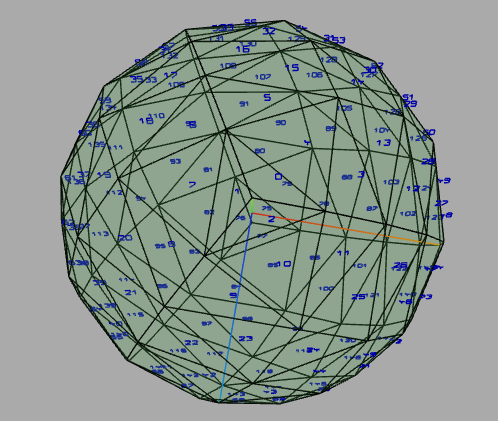 |
| | | | | | |
| | 
HofK | p.specht (27.04.2019)
Könnte man damit das Atomium [...]  in Brüssel nachbauen?
Mit der vorhandene Version wie bereits angemerkt nicht, aber wenn man die Löcher beliebig platzieren kann geht es natürlich.
Die Sache ist naturgemäß etwas komplizierter als bei zu den Koordinatenebenen parallelen Löchern in der Kugel.
Deshalb habe ich erst einmal verschiedene Ansätze getestet. Mit einer non-indexed BufferGeometry verspricht es die günstigste Lösung.
Ein Loch bekommt man schnell in die Kugel, nur kreisförmig muss es noch gemacht werden. Dazu sollte der Ansatz wie bei der effizienten aber nicht symmetrischen Variante (siehe oben) funktionieren.

Zum Test wurden hier die Koordinaten der Punkte des Loches einfach auf 0 gesetzt. Das muss natürlich auch noch etwas bearbeitet werden. |
| | | | | | |
| | 
HofK | Diesmal kein Fehler, sondern ein visueller Test mit noch unvollständiger Berechnung. Da kann man schon mal schauen, ob der eingeschlagene Weg richtig ist. Ein Loch ist zu erkennen. Sieht auch interessant aus.

Die Schwierigkeit beim "Loch machen" besteht darin, dass das Raster nicht äquidistant ist. Mit einer Skalierungsfunktion
const scale = ( k ) => ( k + 0.05 * Math.sin( 2 * Math.PI * k ) ); // j/count scale
kann man das Problem etwas entschärfen, aber nicht vollständig beseitigen. Somit passt der Schnittkreis nicht ins Raster und man muss geeignet ausgleichen. Da probiere ich noch einige Varianten.
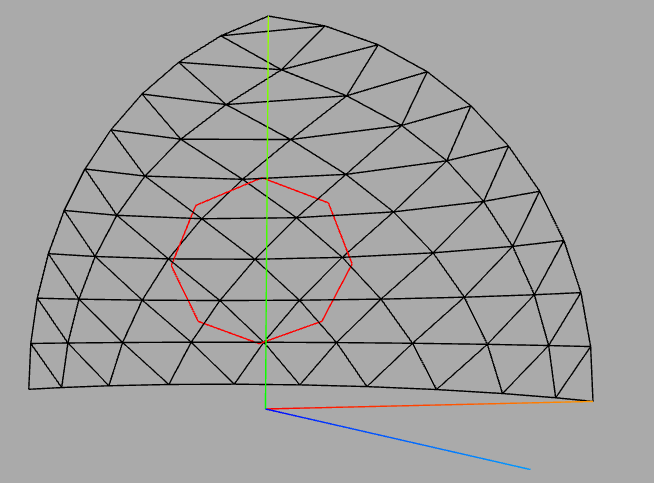
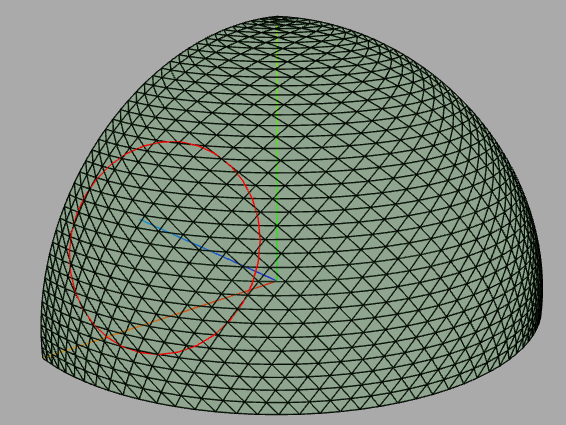
 |
| | | | | | |
| | 
HofK | Die obige Skalierung war rein empirisch. Macht man sich die Mühe und berechnet das Verhältnis von Winkel (Bogen) und entsprechendem Abschnitt der Sehne mit Hilfe des Sinussatzes, erhält man eine exakte Skalierung. Die so bestimmte Funktion sieht auf den ersten Blick der obigen recht ähnlich. Ich habe die Funktion mal mit matheretter.de/tools/funktionsplotter/ [...]  geplottet: geplottet:
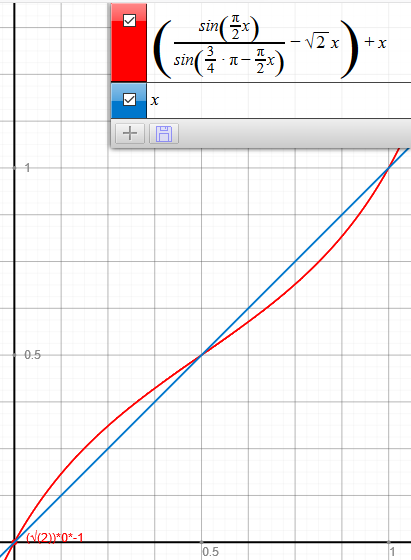
Übrigens benutzt matheretter.de für die Geometrie (geoservant) three.js [...] 
Die Abstände der Knoten sind in jedem einzelnen Ring nun identisch, naturgemäß aber nicht in allen Ringen.
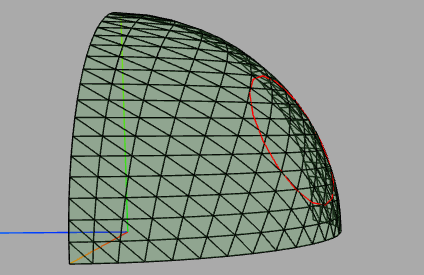
Hier ist Platz für die Einbindung des Schnittkreises und man sieht gerade am Rand den identischen Abstand sehr gut:
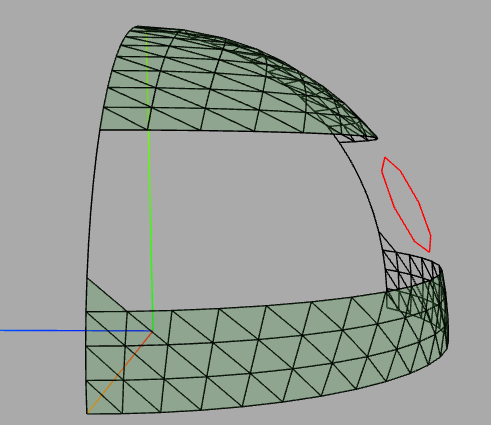
Der linke obere Teil passt schon und man erkennt, dass das Verfahren funktioniert. Der Rest ist Fleißarbeit und Code aufräumen.
 |
| | | | | | |
| | 
p.specht
 | Na da hab´ ich mit meiner Atomium-Frage ja was angerichtet ...  |
| | | | XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 17.05.2019 ▲ |
| | |
| | 
HofK | | | | | | | |
| | 
HofK | 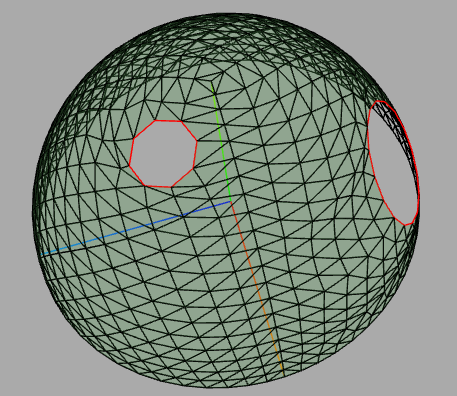
Nun kann man in jedes Teil der Halbkugel an gewünschter Stelle ein Loch "bohren". |
| | | | | | |
| | 
p.specht
 | | | | | Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 21.05.2019 ▲ |
| | |
| | 
HofK | p.specht (21.05.2019)
Coole Bowling-Kugel !
Nur halbe Kugel!

Die Erweiterung auf eine komplette Kugel und die Berechnung von uv-Werten machen noch einmal einen erheblichen Aufwand. Deshalb lasse ich das erst einmal und beschäftige mich lieber mit allgemeineren Verfahren zur Triangulation wie oben angegeben.
Dort kann man die Halbkugel mit Löchern betrachten: [...] 
Der gesamte Code:
<!DOCTYPE html>
<head>
<title> SphereCutAsWanted </title>
<meta charset="utf-8" />
<style>
body {
margin: 0;
}
</style>
</head>
<body> </body>
<script src="../js/three.min.104.js"></script>
<script src="../js/OrbitControls.js"></script>
<script>
// @author hofk
'use strict'
const scene = new THREE.Scene();
const camera = new THREE.PerspectiveCamera( 55, window.innerWidth / window.innerHeight, 0.01, 1000 );
camera.position.set( 3, 1, 2 );
const renderer = new THREE.WebGLRenderer( { antialias: true } );
renderer.setSize( window.innerWidth, window.innerHeight );
renderer.setClearColor( 0xaaaaaa, 1 );
const container = document.createElement('div' );
document.body.appendChild( container );
container.appendChild( renderer.domElement );
const controls = new THREE.OrbitControls( camera, renderer.domElement );
const axesHelper = new THREE.AxesHelper( 1 );
scene.add( axesHelper );
var material1 = new THREE.MeshBasicMaterial( { color: 0x559955, transparent: true, opacity: 0.3, side: THREE.FrontSide, wireframe: false } );
var material2 = new THREE.MeshBasicMaterial( { color: 0x000000, wireframe: true} );
const g = new THREE.BufferGeometry( );
createSphereCut( g, 1.234, 40, 5, [ [ 28, 14, 12 ], [ 10, 6, 4 ], [ ], [ 25, 6, 6 ], [ 32, 6, 4 ] ] );
// BufferGeometry, radius, equator, parts, holes array [ center i, rotary j, radius (even) ] or empty, show circles
const mesh1 = new THREE.Mesh( g, material1 );
scene.add( mesh1 );
const mesh2 = new THREE.Mesh( g, material2 );
scene.add( mesh2 )
animate();
function animate() {
requestAnimationFrame( animate );
renderer.render( scene, camera );
controls.update();
}
function createSphereCut( g, radius, equator, parts, holes, circles ) {
// ..., holes: array [ center i, rotary j, radius (even) ] or empty, optional circles: default is false
// hole parameter from holes aray
let iCenter;// center of hole
let jCenter;// rotary
let rr ;// radius i rings of hole, must be even
let circ = circles !== undefined ? circles : false
const sumON = ( n ) => ( n * n );// Sum odd numbers
const scale = ( k ) => k + Math.sin( pi2 * k ) / Math.sin( 3 * Math.PI / 4 - pi2 * k ) - Math.sqrt(2) * k;
const hCap = ( R ) => ( 1 - Math.sqrt( 1 - R * R ) );// height of spherical cap (cut radius R)
const pi2 = Math.PI / 2;
let eqt = equator;
let hp;// hole part
let iTop, iBtm;
let posIdx, cx, cy, cz, theta, phi ;
let dx, dy, dz, vCount, len;
let holeTopL, holeTopR, holeBtmL, holeBtmR, isHoleL, isHoleR;
let jL = [];
let jR = [];
let positionCount = sumON( eqt ) * parts * 9;// hemisphere
g.positions = new Float32Array( positionCount );
g.addAttribute('position', new THREE.BufferAttribute( g.positions, 3 ) );
let x0 = [];// previus ring
let y0 = [];
let z0 = [];
let x = [];// ring
let y = [];
let z = [];
let lftx = [];// left side positions x
let lfty = [];// left side positions y
let lftz = [];// left side positions z
let rgtx = [];// right side positions x
let rgty = [];// right side positions y
let rgtz = [];// right side positions z
for ( let i = 0; i <= eqt; i ++ ) {// initial (part 0 => left)
theta = pi2 * i / eqt;
rgtx.push( Math.sin( theta ) );
rgty.push( Math.cos( theta ) );
rgtz.push( 0 );
}
let cpLx = [];// circle points
let cpLy = [];
let cpLz = [];
let cpRx = [];
let cpRy = [];
let cpRz = [];
posIdx = 0;
for ( let p = 0; p < parts; p ++ ) {
hp = holes[ p ].length !== 0 ? p : -1;// hole part
iCenter = holes[ p ][ 0 ];// center i of hole
jCenter = holes[ p ][ 1 ];// rotary j
rr = holes[ p ][ 2 ] % 2 === 0 ? holes[ p ][ 2 ] : holes[ p ][ 2 ] + 1;// radius i rings of hole, even
lftx = rgtx.slice( );
lfty = rgty.slice( );
lftz = rgtz.slice( );
rgtx = [];
rgty = [];
rgtz = [];
phi = 2 * Math.PI * ( p + 1 ) / parts;// part right <=> next part left
for ( let i = 0; i <= eqt; i ++ ) {
theta = pi2 * i / eqt;
rgtx.push( Math.sin( theta ) * Math.cos( phi ) );
rgty.push( Math.cos( theta ) );
rgtz.push( -Math.sin( theta ) * Math.sin( phi ) );
}
if ( p === hp ) {
jL = [];
jR = [];
iTop = iCenter - rr;
iBtm = iCenter + rr;
for ( let i = 0; i <= eqt; i ++ ) {// hole structure
areaBordersIndex( i );
}
holeCircle( );// calculate circle positions
}
poleFace( );
x[ 0 ] = lftx[ 1 ];// initial, (first ring)
y[ 0 ] = lfty[ 1 ];// only left
z[ 0 ] = lftz[ 1 ];
x[ 1 ] = rgtx[ 1 ];// and right
y[ 1 ] = rgty[ 1 ];
z[ 1 ] = rgtz[ 1 ];
for ( let i = 1; i < eqt; i ++ ) {
x0 = [];
y0 = [];
z0 = [];
x0 = x.slice( );
y0 = y.slice( );
z0 = z.slice( );
x = [];
y = [];
z = [];
x.push( lftx[ i + 1 ] );
y.push( lfty[ i + 1 ] );
z.push( lftz[ i + 1 ] );
for ( let j = 0; j < i; j ++ ) {
checkHole( p, i, j );
calculatePosition( p, i, j );// position c, without radius
if ( !isHoleL ) {
leftFace( j );
} else {
x.push( cx );
y.push( cy );
z.push( cz );
makeHole( );
}
if ( !isHoleR ) {
rightFace( j );
} else {
makeHole( );
}
}
lastFace( i );// last face, like a left face
}
}
// detail functions
function poleFace( ) {
g.positions[ posIdx ] = radius * lftx[ 0 ];// pole
g.positions[ posIdx + 1 ] = radius * lfty[ 0 ];
g.positions[ posIdx + 2 ] = radius * lftz[ 0 ];
g.positions[ posIdx + 3 ] = radius * lftx[ 1 ];
g.positions[ posIdx + 4 ] = radius * lfty[ 1 ];
g.positions[ posIdx + 5 ] = radius * lftz[ 1 ];
g.positions[ posIdx + 6 ] = radius * rgtx[ 1 ];
g.positions[ posIdx + 7 ] = radius * rgty[ 1 ];
g.positions[ posIdx + 8 ] = radius * rgtz[ 1 ];
posIdx += 9;
}
function leftFace( j ) {
g.positions[ posIdx ] = radius * x0[ j ];// a
g.positions[ posIdx + 1 ] = radius * y0[ j ];
g.positions[ posIdx + 2 ] = radius * z0[ j ];
g.positions[ posIdx + 3 ] = radius * x[ j ];// b
g.positions[ posIdx + 4 ] = radius * y[ j ];
g.positions[ posIdx + 5 ] = radius * z[ j ];
x.push( cx );
y.push( cy );
z.push( cz );
g.positions[ posIdx + 6 ] = radius * cx;// c, new calculated
g.positions[ posIdx + 7 ] = radius * cy;
g.positions[ posIdx + 8 ] = radius * cz;
posIdx += 9;
}
function rightFace( j ) {
g.positions[ posIdx ] = radius * x0[ j ];// a
g.positions[ posIdx + 1 ] = radius * y0[ j ];
g.positions[ posIdx + 2 ] = radius * z0[ j ];
g.positions[ posIdx + 3 ] = radius * cx;// c, see left face
g.positions[ posIdx + 4 ] = radius * cy;
g.positions[ posIdx + 5 ] = radius * cz;
g.positions[ posIdx + 6 ] = radius * x0[ j + 1 ];// a1 ( right from a)
g.positions[ posIdx + 7 ] = radius * y0[ j + 1 ];
g.positions[ posIdx + 8 ] = radius * z0[ j + 1 ];
posIdx += 9;
}
function lastFace( i ) {
// last face, like a left face
g.positions[ posIdx ] = radius * x0[ i ];// a, like j equals i
g.positions[ posIdx + 1 ] = radius * y0[ i ];
g.positions[ posIdx + 2 ] = radius * z0[ i ];
g.positions[ posIdx + 3 ] = radius * cx;// equals last c
g.positions[ posIdx + 4 ] = radius * cy;
g.positions[ posIdx + 5 ] = radius * cz;
cx = rgtx[ i + 1 ];// right side
cy = rgty[ i + 1 ];
cz = rgtz[ i + 1 ];
x.push( cx );
y.push( cy );
z.push( cz );
g.positions[ posIdx + 6 ] = radius * cx;
g.positions[ posIdx + 7 ] = radius * cy;
g.positions[ posIdx + 8 ] = radius * cz;
posIdx += 9;
}
function checkHole( p, i, j ) {
if ( p === hp ) {
holeTopL = i >= iTop && i < iCenter && j >= jL[ i ] && j <= jR[ i ];
holeTopR = i >= iTop && i < iCenter && j >= jL[ i ] && j < jR[ i ];
holeBtmL = i >= iCenter && i < iBtm && j > jL[ i ] && j < jR[ i ];
holeBtmR = i >= iCenter && i < iBtm && j >= jL[ i ] && j < jR[ i ];
isHoleL = holeTopL || holeBtmL;
isHoleR = holeTopR || holeBtmR;
}
}
function makeHole( ) {
for ( let k = 0; k < 9; k ++ ) {
g.positions[ posIdx + k ] = 0;
}
posIdx += 9;
}
function holeCircle( ) {
let lIdx;
cpLx = [];
cpLy = [];
cpLz = [];
cpRx = [];
cpRy = [];
cpRz = [];
theta = theta = pi2 * iCenter / eqt;// refers to ring iCenter ..
phi = 2 * Math.PI / parts * ( hp + jCenter / iCenter );// .. refers to rotary jCenter
cx = Math.sin( theta ) * Math.cos( phi );
cy = Math.cos( theta );
cz = -Math.sin( theta ) * Math.sin( phi );
let r = pi2 * rr / eqt;// without radius of sphere ( = 1 )
let h = hCap( r );
let hc = 1 - h;
// hole circle center point
cx = hc * cx;
cy = hc * cy;
cz = hc * cz;
// unit vectors of cut plane
let e0x = -cx;
let e0y = ( cx * cx + cz * cz ) / cy;
let e0z = -cz;
// cross c , e0
let e1x = cy * e0z - cz * e0y;
let e1y = cz * e0x - cx * e0z;
let e1z = cx * e0y - cy * e0x;
len = Math.sqrt( e0x * e0x + e0y * e0y + e0z * e0z );
e0x = e0x / len;
e0y = e0y / len;
e0z = e0z / len;
len = Math.sqrt( e1x * e1x + e1y * e1y + e1z * e1z );
e1x = e1x / len;
e1y = e1y / len;
e1z = e1z / len;
phi = 0;
if ( circ ) {
let lineGeo = new THREE.BufferGeometry( );
let linesPos = new Float32Array( rr * 4 * 3 );
lineGeo.addAttribute('position', new THREE.BufferAttribute( linesPos, 3 ) );
}
for ( let k = 0; k <= rr * 2; k ++ ) {
cpLx.push( cx + Math.cos( phi ) * r * e0x + Math.sin( phi ) * r * e1x );
cpLy.push( cy + Math.cos( phi ) * r * e0y + Math.sin( phi ) * r * e1y );
cpLz.push( cz + Math.cos( phi ) * r * e0z + Math.sin( phi ) * r * e1z );
if ( circ ) {
linesPos[ k * 3 ] = radius * cpLx[ k ];
linesPos[ k * 3 + 1 ] = radius * cpLy[ k ];
linesPos[ k * 3 + 2 ] = radius * cpLz[ k ];
}
phi += pi2 / rr;// equals 2 * PI / ( 4 * rr )
}
phi = 2 * Math.PI;
for ( let k = 0; k <= rr * 2; k ++ ) {
lIdx = ( 4 * rr - k - 1 ) * 3;
cpRx.push( cx + Math.cos( phi ) * r * e0x + Math.sin( phi ) * r * e1x );
cpRy.push( cy + Math.cos( phi ) * r * e0y + Math.sin( phi ) * r * e1y );
cpRz.push( cz + Math.cos( phi ) * r * e0z + Math.sin( phi ) * r * e1z );
if ( circ ) {
linesPos[ lIdx + 3 ] = radius * cpRx[ k ];
linesPos[ lIdx + 4 ] = radius * cpRy[ k ];
linesPos[ lIdx + 5 ] = radius * cpRz[ k ];
}
phi -= pi2 / rr;// equals 2 * PI / ( 4 * rr )
}
if ( circ ) {
let lineMaterial = new THREE.LineBasicMaterial({ color: 0xff0000 });
let line = new THREE.LineLoop( lineGeo, lineMaterial );
scene.add( line );
}
}
function areaBordersIndex( i ) {
if ( i < iTop ) {
jL.push( i );
jR.push( i );
}
if ( i >= iTop && i < iCenter ) {
jL.push( jCenter - rr / 2 );
jR.push( jCenter + rr / 2 + i - iCenter );
}
if ( i >= iCenter && i <= iBtm ) {
jL.push( jCenter - rr / 2 + i - iCenter );
jR.push( jCenter + rr / 2 );
}
if ( i > iBtm ) {
jL.push( i );
jR.push( i );
}
}
function calculatePosition( p, i, j ) {
let dj1, dji, t;
// refers to next ring
let i1 = i + 1;
let idx1 = i - iTop + 1;
if ( i >= iTop - 1 && i <= iBtm - 1 && p === hp ) {
if ( j < jL[ i1 ] ) {
dx = cpLx[ idx1 ] - lftx[ i1 ];
dy = cpLy[ idx1 ] - lfty[ i1 ];
dz = cpLz[ idx1 ] - lftz[ i1 ];
vCount = jL[ i1 ] + 1;
dj1 = ( j + 1 ) / ( vCount - 1 );
cx = lftx[ i1 ] + dj1 * dx;
cy = lfty[ i1 ] + dj1 * dy;
cz = lftz[ i1 ] + dj1 * dz;
}
if ( j >= jL[ i1 ] && j < jR[ i1 ] ) {
dx = cpRx[ idx1 ] - cpLx[ idx1 ];
dy = cpRy[ idx1 ] - cpLy[ idx1 ];
dz = cpRz[ idx1 ] - cpLz[ idx1 ];
vCount = jR[ i1 ] - jL[ i1 ] + 1;
dji = ( ( j - jL[ i1 ] + 1 ) ) / ( vCount - 1 );
cx = cpLx[ idx1 ] + dji * dx;
cy = cpLy[ idx1 ] + dji * dy;
cz = cpLz[ idx1 ] + dji * dz;
}
if ( j >= jR[ i1 ] ) {
dx = rgtx[ i1 ] - cpRx[ idx1 ];
dy = rgty[ i1 ] - cpRy[ idx1 ];
dz = rgtz[ i1 ] - cpRz[ idx1 ];
vCount = i1 - jR[ i1 ] + 1;
dji = ( ( j - jR[ i1 ] + 1 ) ) / ( vCount - 1 );
cx = cpRx[ idx1 ] + dji * dx;
cy = cpRy[ idx1 ] + dji * dy;
cz = cpRz[ idx1 ] + dji * dz;
}
}
if ( i < iTop - 1 || i > iBtm - 1 || p !== hp ) {
dx = rgtx[ i1 ] - lftx[ i1 ];
dy = rgty[ i1 ] - lfty[ i1 ];
dz = rgtz[ i1 ] - lftz[ i1 ];
vCount = ( i1 ) + 1;
// scale
dj1 = scale( ( j + 1 ) / ( vCount - 1 ) );
cx = lftx[ i1 ] + dj1 * dx;
cy = lfty[ i1 ] + dj1 * dy;
cz = lftz[ i1 ] + dj1 * dz;
}
t = Math.sqrt( ( 1 - cy * cy ) / ( cx * cx + cz * cz ) );// to move the point horizontally onto the sphere
cx = cx * t;
cz = cz * t;
}
}
</script>
</html>
|
| | | | | | |
| | 
HofK |
Das braucht etwas Zeit. Das Verfahren [...] 
ist etwas kompliziert und muss tiefgründig durchdrungen werden und der Code [...]  ist in Pascal. Damit habe ich mich letztmalig vor über 10 Jahren befasst. ist in Pascal. Damit habe ich mich letztmalig vor über 10 Jahren befasst.
Für den konkreten und einfachen Fall der Kugel möchte ich darüber hinaus eine angepasste und damit im Rechenaufwand reduzierte Variante erstellen. So ist bei einer Kugel der Normalenvektor stets identisch mit dem Ortsvektor des Kugelpunktes. Die Krümmung der Kugeloberfläche ist überall konstant.
Dadurch kann man einfachere Verfahren für bestimmte Schritte anwenden oder Schritte weglassen.
Einige Dinge muss ich noch testen, z.B. ob sie praktikabel sind und tatsächlich den Aufwand gegenüber dem originalen, allgemeinen Algorithmus verringern.
Bei den Tests erhält man ganz nebenbei aber auch einige interessante Erkenntnisse.
Ein Testbeispiel mit zwei Dreiecken und einigen Vektoren. Als Basis eine einfache Kugel nach three.js Definition (Gelb).
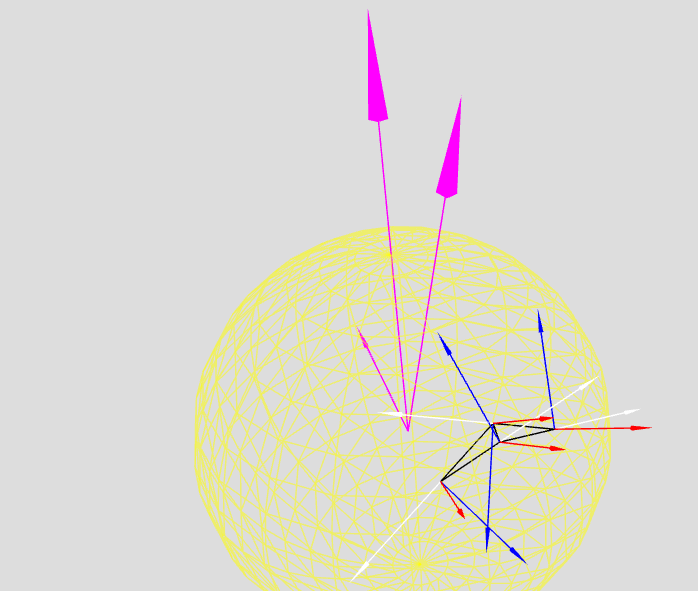 |
| | | | | | |
|
AntwortenThemenoptionen | 394.957 Betrachtungen |
ThemeninformationenDieses Thema hat 10 Teilnehmer: |