| |
| |
|
| - Seite 1 - |
|

HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
|
| |
| |
| |
|
| |
| |
| - Seite 29 - |
|
|

HofK |  So wie ich es an meinem Schreibtisch mache. Mann muss nur aufpassen, dass die ganze Elektronik keine feuchten Füße bekommt. So wie ich es an meinem Schreibtisch mache. Mann muss nur aufpassen, dass die ganze Elektronik keine feuchten Füße bekommt.
Übrigens fehlt mir noch das Vasenloch. Zwei Zylinder die im Winkel ungleich 90° aufeinander treffen. Mal schauen, ob ich einen Ansatz finde. |
|
| |
| |
| |
|
|

HofK | Ansatz scheint machbar. Aber bei meinen Schusselfehlern 
Eventuell möchte jemand nachrechnen  , ehe ich es programmiere und eigenartige Formen herauskommen??? , ehe ich es programmiere und eigenartige Formen herauskommen???
 |
|
| |
| |
| |
|
|

p.specht
 | Maxima [...]  ist ähnlich wie Mathematica, aber gratis! Von dort stammt auch die Quartische Formel da oben. Mittels Maxima konnte ich viele Fehler vermeiden bzw. rechtzeitig erkennen. Bei mir ging es aber nur um eine abrollende Elllipse... ist ähnlich wie Mathematica, aber gratis! Von dort stammt auch die Quartische Formel da oben. Mittels Maxima konnte ich viele Fehler vermeiden bzw. rechtzeitig erkennen. Bei mir ging es aber nur um eine abrollende Elllipse... |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 02.11.2019 ▲ |
|
| |
|
|

HofK | Da habe ich wohl am gestrigen Abend bei der Lösung der quadratischen Gleichung nicht geschusselt:
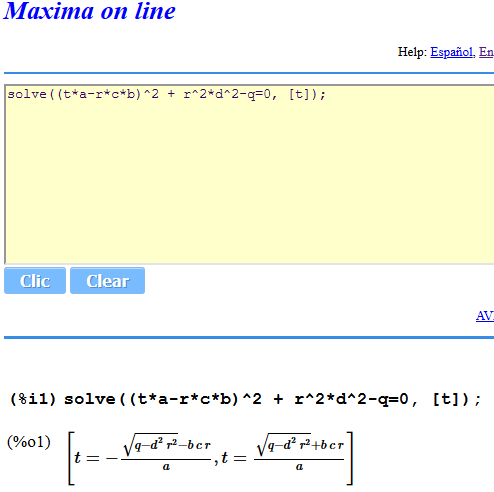
Ob der Ansatz allerdings stimmt, wird sich am 3D-Ergebnis zeigen.
Nettes Tool, sollte ich mal bei Gelegenheit einige meiner dubiosen Integralansätze auf geschlossene Lösbarkeit prüfen.
Ansonsten mache ich Ansatz-Lösung gern selbst, hält den Geist frisch. |
|
| |
| |
| |
|
|

HofK | Wenn ich Exzentrik und Winkel kombiniere, wird es nicht komplizierter.
Dabei sieht man, was mich zuweilen bei automatischen Lösungen stört. Durch Umbenenung eines Bezeichners entsteht eine andere Reihenfolge.
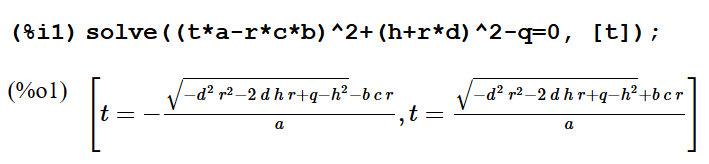
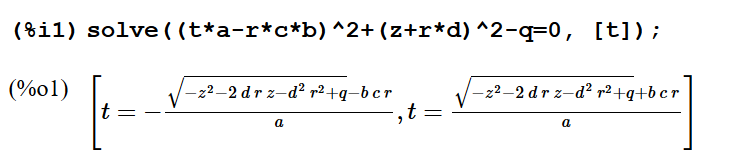
Außerdem löse ich das Binom (z+rd)^2 nicht auf und erhalte
q - (z+rd)^2 unter der Wurzel, was übersichtlicher erscheint. q ist das R zum Quadrat.
Übrigens habe ich am gestrigen Abend doch geschusselt, in einer Zeile fehlt das hoch 2 am R! In der nächsten Zeile taucht es wieder auf. |
|
| |
| |
| |
|
|

p.specht
 | Wusste garnicht, daß es Maxima inzwischen auch online gibt! Die Kerle kupfern bei Mathematica (bzw. Wolfram Alpha) ab...
Die Ergebnisse sind leider bei Computeralgebra-Systemen nie direkt programmier-geeignet. Kanonisieren, memoisieren, Werte zwischenspeichern falls sinnvoll, Laufzeit optimieren - das muss man leider alles selber machen. |
|
| |
| Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 02.11.2019 ▲ |
|
| |
|
|

HofK | " Ob der Ansatz allerdings stimmt, wird sich am 3D-Ergebnis zeigen."
Nach dem obligatorischen "spanischem Halskrausen"-Fehler

klappt es mit dem Ansatz.

Bei der einfachen Rechnung über den umlaufenden Winkel wird die starke Verzerrung deutlich. Wenn bei größerer Exzentrik der zweite Zylinder teilweise am ersten vorbei geht, benötigt man ohnehin die iterative Variante.
Gegenüber der Kugel wird es noch einmal komplizierter, da keine Symmetrie mehr vorliegt und man nicht einfach spiegeln kann. Es sind mehrere unabhängige Rechnungen nötig. Für Arbeit ist also gesorgt. |
|
| |
| |
| |
|
|

p.specht
 | | Muss die allfällige Textur an der Position der Loches transparent sein, oder wird dieser Teil gar nicht gerendert? |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 02.11.2019 ▲ |
|
| |
|
|

HofK | Gerändert werden nur die Dreiecke, die ich hier zur Sichtbarmachung doppelt zeichne. Einmal Grün, transparent und einmal "wireframe", also nur Seiten in schwarz. Möchte man das Loch anders füllen, muss man da auch Dreiecke erzeugen und andere Farben zuweisen. Weiter oben ist ja als Fehler ein gefülltes Loch zu sehen.
-------------
Wie stabil der Algorithmus von E.Hartmann ist, sieht man bei dem extrem schräg schneidendem Zylinder an den starken Verzerrungen. Aber das muss man mit der iterativen Variante verbessern.
 |
|
| |
| |
| |
|
|

p.specht
 | Ich ´frug´ wegen ´Wasserspiegel steigen lassen´. Rendering mittels einer Textur hat mit Rändern natürlich wenig zu tun  . Die Dreiecke liegen m.E. an sich richtig - im Sinne künftiger Anwendungen wie Finite Elemente Methode o.Ähnl. . Die Dreiecke liegen m.E. an sich richtig - im Sinne künftiger Anwendungen wie Finite Elemente Methode o.Ähnl. |
|
| |
| Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 03.11.2019 ▲ |
|
| |
|
|

HofK | Die iterative Variante klappt erstmal soweit der zweite Zylinder den ersten Zylinder vollständig durchdringt. Dabei konnte ich die Berechnung in "einem Rutsch" über den vollen Kreis realisieren.
Die Variante für die teilweise Durchdringung ist noch in Arbeit.
Auch wieder einige schöne Fehlversuche.

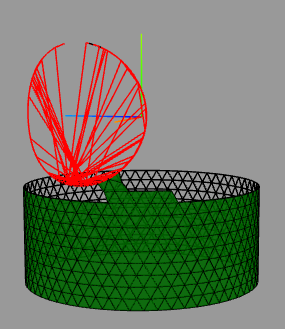
Die Dreiecksseiten am Loch haben die richtige Länge.
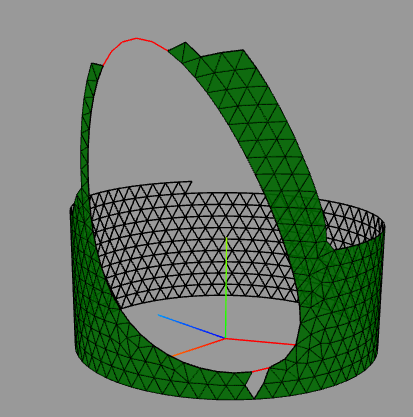
 |
|
| |
| |
| |
|
|

p.specht
 | | Bitte kann man auf die Längen der automatisch erzeugten Rand-Dreiecksseiten irgendwie zugreifen (Ich frage wegen Kräfteparallelogrammen etc)? |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 10.11.2019 ▲ |
|
| |
|