| |
| |
|
| - Seite 1 - |
|

HofK | Auf einen heißen  Tipp von IF hin, habe ich mir mal Tipp von IF hin, habe ich mir mal
three.js [...]  angeschaut. Da [...] angeschaut. Da [...]  (ganz unten) die ersten Resultate. (ganz unten) die ersten Resultate. |
|
| |
| |
| |
|
| |
| |
| - Seite 30 - |
|
|

HofK | Alle Ecken der Dreiecke sind im Pufferfeld der Positionen gespeichert.
Somit kann man beliebige Längen berechnen, wenn man die benötigten Indizes hat.
Aus verschiedenen Gründen speichere ich die primären Positionen für die Löcher in einem normalen array let pos = []; mittels pos.push( x, y, z ); zwischen.
Damit berechnen sich die Längen sehr einfach. Da die Löcher auch stärkere Krümmungen enthalten, habe ich den Iterationsabbruch auf 90% der ungefähren Seitenlänge der Dreiecke gesetzt.
////////// console //////////////////////////////////////////////
let lx,ly,lz;
console.log('g.d', g.d ); //// rough side length of the triangles
for ( let i = 3; i < pos.length; i += 3 ) {// uses sqlen0 < 0.81 * dd, equals 0.9*d
lx = pos[ i ] - pos[ i - 3 ];
ly = pos[ i + 1 ] - pos[ i - 2 ];
lz = pos[ i + 2 ] - pos[ i - 1 ];
console.log('length',length( lx, ly, lz) ); // 0.9*d = 0.135
}
////////////////////////////////////////////////////////////////////
Für dieses kleine Löchlein ergeben sich folgende Werte.
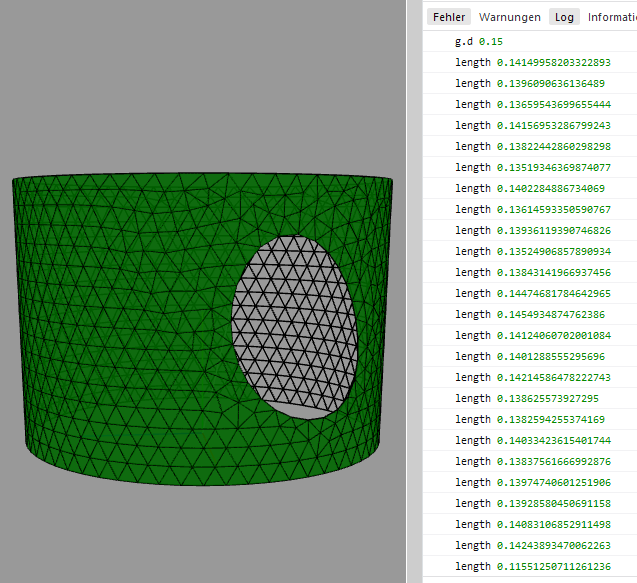 |
|
| |
| |
| |
|
|

p.specht
 | Danke, das gibt´s also. Für FEM etc. müsste man noch die Richtungen wissen. Aber das bleibt ohnehin Spezialisten überlassen. Da in der representation nur Flächen vorkommen, es dort aber auf Trägheitsmomente, Massenverteilungen, Materialsteifigkeiten etc. ankommt, bleibt das hier Zukunftsmusik. War auch nur so eine Idee - ich hatte mal ein 16bit-Programm für FEM, das ganz gut war. Läuft natürlich nicht mehr.
Gruss |
|
| |
| Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 11.11.2019 ▲ |
|
| |
|
|

HofK | | Mit FEM (Finite-Elemente-Methode) habe ich mich nicht beschäftigt. Da benötigt man aber Teilkörperchen des Gesamtkörpers. Meine "Körper" sind nur Oberflächen. Die Löcher erzeuge ich für die Innengeometrie, siehe Beitrag vom 25.09. Ansonsten kann man die zusammengesetzten Oberflächen einfach durch Überschneidung generieren. |
|
| |
| |
| |
|
|

HofK | Die bisher noch fehlenden Varianten Zylinder-Zylinder sind soweit fertig.
Ein verbundenes Loch:


Zwei Löcher:
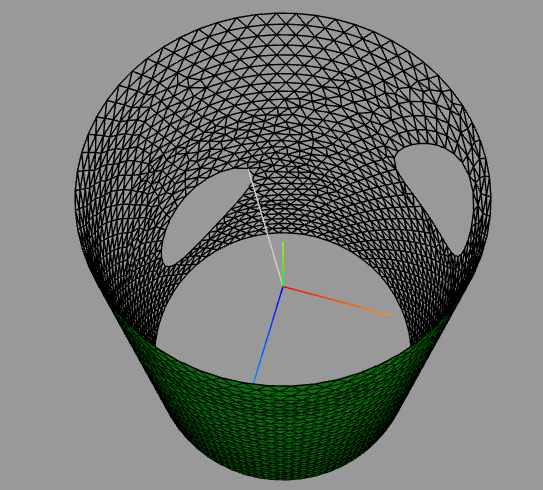
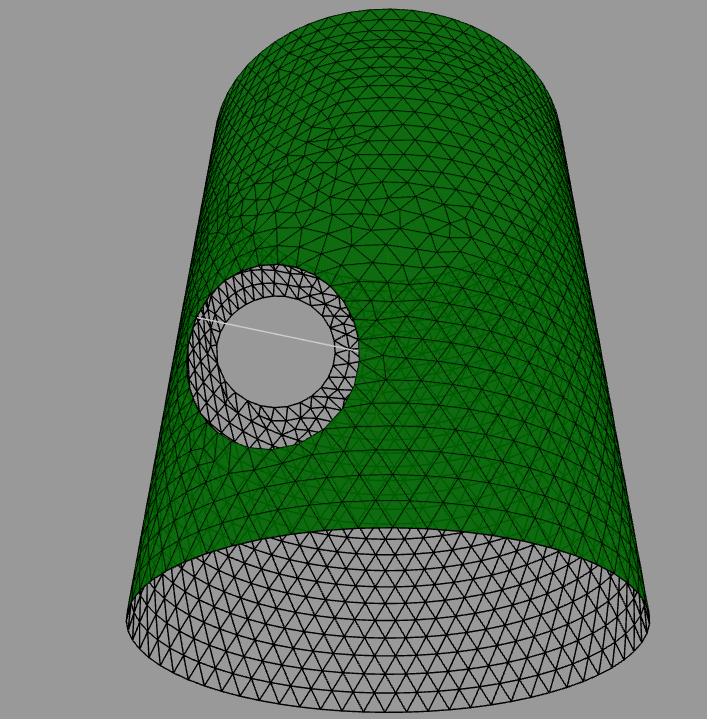
Knappe Sache:

Nun noch etwas Fleißarbeit beim Aufräumen und optimieren des Codes. |
|
| |
| |
| |
|
|

p.specht
 | |
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 16.11.2019 ▲ |
|
| |
|
|

HofK | |
| |
| |
| |
|
|

p.specht
 | Laufmasche, sozusagen ... Wie wär´s mit einem Ausgleichsstück, überlagernd? Zuschweissen wird wohl eher nicht gelingen  |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 20.11.2019 ▲ |
|
| |
|
|

HofK | Ich hatte eher an kleben gedacht, aber das verschmiert das Display. Lötzinn würde wohl abperlen und schweißen wäre bei einem alten Röhrenmonitor sicher ein schönes Implosions-Experiment.
Also dann doch lieber meinen Soft-JavaScript-Tacker benutzen!
Das Problem liegt in den leicht unterschiedlichen Umsetzungen der Iteration. Da ich es für die unterschiedlichen Fronten nacheinander experimentell ermittelt habe, gibt es feine Unterschiede im Algorithmus. Zur Optimierung des Codes muss das ohnehin vereinheitlicht werden, um ähnliche /identische Codeabschnitte nicht mehrfach zu haben.
Der gegenwärtige Stand ergibt die folgende allgemeine Funktion
function makeFrontPos( xyzCalc ).
Dieser wird die konkrete Funktion für die Schnittlinie übergeben
function xyzCalcSphHole( ) für die Kugel (Schnitt mit Zylinder).
Ausgangswerte werden in der Triangulations-Hauptfunktion gesetzt um Parameterübergaben zu sparen. Das entspricht meiner Vorgehensweise beim Triangulationsprojekt.
Nätürlich anfangs wieder eine schöne Fehldarstellung. Sie zeigt nochmals die hohe Stabilität der Triangulation bei fehlerhaften Fronten.

function makeFrontPos( xyzCalc ) {
psi = psiStart;
dpsi = Math.PI * 2 / g.detail / 16;
sqlen1 = 9 * dd;// initial
xyzCalc( );// start point
pos.push( x, y, z );
// notice start point
x0 = x;
y0 = y;
z0 = z;
if ( psi !== psiEnd ) {
psi = psiEnd;
xyzCalc( );
psi = psiStart;// initial again
}
// notice endpoint to check finish
x1 = x;
y1 = y;
z1 = z;
while ( sign > 0 ? psi < psiEnd && ( sqlen1 > 5.76 * dd || psi < ( psiEnd - psiStart ) / 2 ) : psi > psiEnd && ( sqlen1 > 5.76 * dd || psi > ( psiStart - psiEnd ) / 2 ) ) {
// (adaptive-deformed) circle
psi0 = psi;
sqlen0 = 0;
while ( sqlen0 < 0.81 * dd ) {
psi += sign * dpsi;
xyzCalc( );
dx = x - x0;
dy = y - y0;
dz = z - z0;
sqlen0 = squareLength( dx, dy, dz );
}
pos.push( x, y, z );
if ( slope ='dx' ) {
dyzdx = Math.abs( Math.sqrt( dy * dy + dz * dz ) / dx );
dyzdx = dyzdx > 1 ? 1 : dyzdx;
dpsi = Math.abs( psi - psi0 ) * dyzdx / 16;
} else {// 'dy'
dxzdy = Math.abs( Math.sqrt( dx * dx + dz * dz ) / dy );
dxzdy = dxzdy > 1 ? 1 : dxzdy;
dpsi = Math.abs( psi - psi0 ) * dxzdy / 16;
}
x0 = x;
y0 = y;
z0 = z;
dx = x - x1;
dy = y - y1;
dz = z - z1;
sqlen1 = squareLength( dx, dy, dz );
}
// possibly a intermediate point
if( sqlen1 > 1.44 * dd ) {
psi += ( psiEnd - psi ) / 2 ;
/* or
a = y1 === 0 ? 3 : 2;
psi += a * ( psiEnd - psi ) / 4;
*/
xyzCalc( );
pos.push( x, y, z );
}
if( !openFrt ) pos.push( x1, y1, z1 );
}
 |
|
| |
| |
| |
|
|

HofK | Die Ergänzung der Fronten zur Anpassung von Zylinder und Kugel an die Enden des Zylinders hat mehr Arbeit gemacht als gedacht.
Aber so sieht es ganz praktikabel aus.


Die Parameter des Beispiels. Unten passt ein Zylinder dran, oben eine Kugel.
const parameters = {
d: 0.15,// rough side length of the triangles
div4: 15,// division of the quarter circle
geoBtm:'cylinder', // 'cylinder', 'sphere', solid to be adapted
bottom: -3.0,
div4Btm: 34,// division bottom adaptation, (to quarter, >= div4)
phiBtm: 0,// rotation of adaptive-deformed circle (Bottom)
excBtm: 1.8049,
//tiltBtm: 0.0, // tilt of bottom adaption ( -PI/2 < tilt < PI/2 )
geoTop:'sphere', // 'sphere', solid to be adapted
top: 1.0,
div4Top: 34,// division top adaptation, (to quarter, >= div4)
phiTop: 0,// rotation of adaptive-deformed circle (Top)
excTop: 1.8049,
//tiltTop: 0.0, // tilt of top adaption ( -PI/2 < tilt < PI/2 )
holes: [
// unit: '%' of the radius, 'd' factor to d, 'v' value
// hole to conect a sphere: [ 'sphere', div4AdpSph, y, phi, exc, unit ]
['sphere', 16, -1.11, 0, 2.686, 'v' ],
// hole to conect a cylinder: [ 'cylinder', div4AdpCyl, y, phi, exc, unit, tilt, <optional: side> ]
['cylinder', 8, -2.2, 1.57, 50, '%', -0.22, '+-' ],
//points hole,: array of points y, phi, ... (last point is connected to first)
[ 0.15,0.45, 0.5,0.9, 0.8,0.6, 0.75,-0.2, 0.1,-0.15 ]
]
}
Es waren einige Funktionen zu gestalten.

Nun sind noch "Restarbeiten" nötig.  |
|
| |
| |
| |
|
|

p.specht
 | | Gratulation! Das war sicher eine grössere Hürde! Jetzt wären wahrscheinlich sowas wie Makros hilfreich, die die Fälle unterscheiden helfen - sonst bleibt es Hand-/Kopfarbeit. Wie sieht es übrigens mit Bemaßung aus? |
|
| |
| XProfan 11Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 08.12.2019 ▲ |
|
| |
|
|

HofK | Bemaßungen sind kein Problem, habe ich aber nicht vorgesehen. Man zeichnet Linien und kleine Dreiecke als Spitzen. Die Ziffern kann man auf unterschiedliche Weise erzeugen. Beispielsweise so, wie ich es für meine NumbersHelper gemacht habe, z.B. [...] 
Zwischendurch habe ich nach langer Zeit wieder mal shader betrachtet. [...] 
und mir noch eine andere Sache "eingehandelt" als ich über einen kleinen Fehler gestolpert bin. [...]  |
|
| |
| |
| |
|
|

p.specht
 | Maßzahlen, die nicht mitdrehen: Wow, super!
Wie könnte man eine Schnittebene in das Objekt legen, sodaß nur der dahinter-befindliche Teil gezeichnet wird (z.B. Stockwerkspläne) ? |
|
| |
| Computer: Gerät, daß es in Mikrosekunden erlaubt, 50.000 Fehler zu machen, zB 'daß' statt 'das'... | 10.12.2019 ▲ |
|
| |
|